题目内容
16.若sin$\frac{α}{2}$=-$\frac{1}{2}$,α∈[2π,3π],则α=$\frac{7π}{3}$.分析 直接利用已知条件求出终边相同的角的表达式,然后求解即可.
解答 解:sin$\frac{α}{2}$=-$\frac{1}{2}$,可得$\frac{α}{2}$=2k$π-\frac{π}{6}$,或$\frac{α}{2}$=2k$π-\frac{5π}{6}$,k∈Z,
可得:α=4k$π-\frac{π}{3}$,或α=4k$π-\frac{5π}{3}$,k∈Z,∵α∈[2π,3π],∴α=$\frac{7π}{3}$.
故答案为:$\frac{7π}{3}$.
点评 本题考查三角函数的化简求值,考查计算能力.

练习册系列答案
相关题目
7.已知三棱锥P-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,PC为球O的直径,该三棱锥的体积为$\frac{\sqrt{2}}{6}$,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
4.下列函数中,没有零点的是( )
| A. | f(x)=0 | B. | f(x)=2 | C. | f(x)=x2-1 | D. | f(x)=x-$\frac{1}{x}$ |
1.设f(x)为二次函数,且不等式f(x)>0之解为-2<x<4,则f(2x)<0之解为( )
| A. | -1<x<2 | B. | x<-1或x>2 | C. | x<-1或x>4 | D. | -4<x<8 | ||||
| E. | x<-4或x>8 |
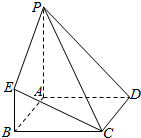 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.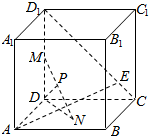 已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.
已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.