题目内容
14.正四棱柱ABCD-A1B1C1D1中,底面边长为2,截面AB1C1D与底面ABCD所成二面角的正切值为2,则B1点到平面AD1C的距离为( )| A. | $\frac{8}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{4}{3}$ |
分析 由AB1⊥AD,AB⊥AD,知∠BAB1是截面AB1C1D与底面ABCD所成二面角,由截面AB1C1D与底面ABCD所成二面角的正切值为2,求出BB1=2AB=4,以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出B1点到平面AD1C的距离.
解答 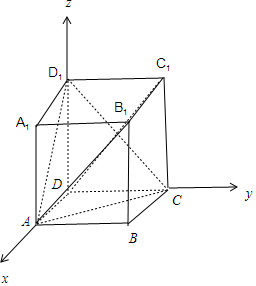 解:∵正四棱柱ABCD-A1B1C1D1中,底面边长为2,
解:∵正四棱柱ABCD-A1B1C1D1中,底面边长为2,
∴AB1⊥AD,AB⊥AD,
∴∠BAB1是截面AB1C1D与底面ABCD所成二面角,
∵截面AB1C1D与底面ABCD所成二面角的正切值为2,
∴tan∠BAB1=$\frac{B{B}_{1}}{AB}$=2,∴BB1=2AB=4,
以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A(2,0,0),C(0,2,0),D1(0,0,4),B1(2,2,4),
$\overrightarrow{A{D}_{1}}$=(-2,0,4),$\overrightarrow{AC}$=(-2,2,0),$\overrightarrow{A{B}_{1}}$=(0,2,4),
设平面AD1C的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=-2x+4z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-2x+2y=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(2,2,1),
∴B1点到平面AD1C的距离:
d=$\frac{|\overrightarrow{n}•\overrightarrow{A{B}_{1}}|}{|\overrightarrow{n}|}$=$\frac{8}{3}$.
故选:A.
点评 本题考查点到平面的距离、二面角等基础知识,考查推理论证能力、运算求解能力、空间想象能力、数据处理能力,考查函数与方程思想、化归与转化思想、数形结合,考查创新意识、应用意识,是中档题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| x | 0 | 1 | m | 3 |
| y | 1 | 3 | 5 | n |
| A. | $({\frac{4π}{3},0})$ | B. | $({\frac{π}{2},0})$ | C. | $({\frac{π}{3},0})$ | D. | $({\frac{π}{6},0})$ |
| A. | $(\frac{1}{2},1]$ | B. | $(0,\frac{2}{3})$ | C. | $(\frac{2}{3},1]$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
