题目内容
9.函数$y=2cos({\frac{1}{2}x+\frac{π}{3}})$图象的一个对称中心为( )| A. | $({\frac{4π}{3},0})$ | B. | $({\frac{π}{2},0})$ | C. | $({\frac{π}{3},0})$ | D. | $({\frac{π}{6},0})$ |
分析 由题意,令$\frac{1}{2}$x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,可得对称中心为(2kπ+$\frac{π}{3}$,0),k∈Z,即可得出结论.
解答 解:令$\frac{1}{2}$x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,可得对称中心为(2kπ+$\frac{π}{3}$,0),k∈Z,
k=0,对称中心为($\frac{π}{3}$,0),
故选:C.
点评 本题考查正弦函数的对称中心,体现了转化的数学思想,比较基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20.已知m.n是两条不同直线,α,β是两个不同的平面,则下列题是真命题的是( )
| A. | 若m∥n,m∥β,则 n∥β | B. | 若m∥β,α⊥β,则 m⊥α | ||
| C. | 若m∥n,m⊥β,则n⊥β | D. | 若m?α,n?β,α∥β,则 n∥m |
14.正四棱柱ABCD-A1B1C1D1中,底面边长为2,截面AB1C1D与底面ABCD所成二面角的正切值为2,则B1点到平面AD1C的距离为( )
| A. | $\frac{8}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{4}{3}$ |
1.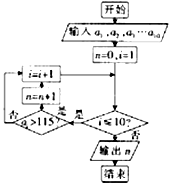 某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
 某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 门票收入(万元) | 80 | 120 | 110 | 91 | 65 | 77 | 131 | 116 | 55 | 77 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.某几何体的三视图如图所示,该几何体的体积为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
19.下列函数中不是偶函数的是( )
| A. | y=sin|x| | B. | y=-|sinx| | C. | y=cosx+1 | D. | y=sin2x |
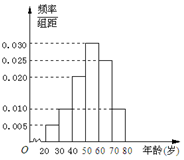 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.