题目内容
设数列{an}的各项均为正数,它的前n项的和为Sn,点(an,Sn)在函数y=
x2+
x+
的图象上;数列{bn}满足b1=a1,bn+1•(an+1-an)=bn,其中n∈N*.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
,求数列{cn}的前n项的和Tn.
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
| an |
| bn |
考点:数列的求和,数列的应用
专题:等差数列与等比数列
分析:(1)由已知条件得Sn=
an2+
an+
,从而an-an-1=4(n≥2),又a1=2,由此得到an=4n-2,从而b1=2,
=
,由此得到bn=2•(
)n-1.
(2)由cn=
=(2n-1)•4n-1,利用错位相减法能求出数列{cn}的前n项的和Tn.
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| bn+1 |
| bn |
| 1 |
| 4 |
| 1 |
| 4 |
(2)由cn=
| an |
| bn |
解答:
解:(1)∵数列{an}的各项均为正数,它的前n项的和为Sn,
点(an,Sn)在函数y=
x2+
x+
的图象上,
∴由已知条件得Sn=
an2+
an+
,①
当n≥2时,Sn-1=
an-12+
an-1+
,②
①-②得:an=
(an2-an-12)+
(an-an-1),
即an+an-1=
(an+an-1)(an-an-1),
∵数列{an}的各项均为正数,∴an-an-1=4(n≥2),
又a1=2,∴an=4n-2,
∵b1=a1,bn+1(an+1-an)=bn,
∴b1=2,
=
,∴bn=2•(
)n-1.
(2)∵cn=
=(2n-1)•4n-1,
∴Tn=1+3•4+5•42+…+(2n-1)•4n-1,
4Tn=4+3•42+5•43+…+(2n-1)•4n,
两式相减得-3Tn=1+2(4+42+43+…+4n-1)-(2n-1)•4n
=1+2×
-(2n-1)•4n
=-
-(2n-
)•4n,
∴Tn=
+
•4n.
点(an,Sn)在函数y=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
∴由已知条件得Sn=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,Sn-1=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:an=
| 1 |
| 8 |
| 1 |
| 2 |
即an+an-1=
| 1 |
| 4 |
∵数列{an}的各项均为正数,∴an-an-1=4(n≥2),
又a1=2,∴an=4n-2,
∵b1=a1,bn+1(an+1-an)=bn,
∴b1=2,
| bn+1 |
| bn |
| 1 |
| 4 |
| 1 |
| 4 |
(2)∵cn=
| an |
| bn |
∴Tn=1+3•4+5•42+…+(2n-1)•4n-1,
4Tn=4+3•42+5•43+…+(2n-1)•4n,
两式相减得-3Tn=1+2(4+42+43+…+4n-1)-(2n-1)•4n
=1+2×
| 4(1-4n-1) |
| 1-4 |
=-
| 5 |
| 3 |
| 5 |
| 3 |
∴Tn=
| 5 |
| 9 |
| (6n-5) |
| 9 |
点评:本题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想,解题时要注意错位相减法的合理运用.

练习册系列答案
相关题目
若sinθ+cosθ=
,则tan(θ+
)的值是( )
| 2 |
| π |
| 3 |
| A、1 | ||
B、-
| ||
C、-1+
| ||
D、-
|
在矩形ABCD中,|
|=
,|
|=1,则|
-
|=( )
| AB |
| 3 |
| BC |
| BA |
| BC |
| A、2 | ||
| B、3 | ||
C、2
| ||
| D、4 |
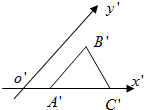 如图是水平放置的△ABC的直观图,A′B′∥y′轴,A′B′=A′C′,则△ABC是( )
如图是水平放置的△ABC的直观图,A′B′∥y′轴,A′B′=A′C′,则△ABC是( )| A、等边三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |