题目内容
已知数列{an}为等差数列,a5=11,且a4+a8=26.
(Ⅰ)求数列{an}的通项;
(Ⅱ)设bn=2an-an,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项;
(Ⅱ)设bn=2an-an,求数列{bn}的前n项和Sn.
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用等差数列的性质列出方程组,求出首项和公差,由此能求出an=2n+1.
(Ⅱ)由bn=2an-an=22n+1-(2n+1),由此利用分组求和法能求出数列{bn}的前n项和Sn.
(Ⅱ)由bn=2an-an=22n+1-(2n+1),由此利用分组求和法能求出数列{bn}的前n项和Sn.
解答:
(本题满分13分)
解:(Ⅰ)设{an}的公差为d,
则a5=a1+4d=11,a1+3d+a1+7d=26
解得a1=3,d=2…(4分)
所以an=2n+1…(5分)
(Ⅱ)∵bn=2an-an=22n+1-(2n+1)…(2分)
Sn=b1+b2+…+bn=(23+25+…+22n+1)-[3+5+…+(2n+1)]…(4分)
=
-
×n…(6分)
=
(22n+3-8)-n2-2n…(8分)
解:(Ⅰ)设{an}的公差为d,
则a5=a1+4d=11,a1+3d+a1+7d=26
解得a1=3,d=2…(4分)
所以an=2n+1…(5分)
(Ⅱ)∵bn=2an-an=22n+1-(2n+1)…(2分)
Sn=b1+b2+…+bn=(23+25+…+22n+1)-[3+5+…+(2n+1)]…(4分)
=
| 23(1-4n) |
| 1-4 |
| 3+2n+1 |
| 2 |
=
| 1 |
| 3 |
点评:本题主要考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想.

练习册系列答案
相关题目
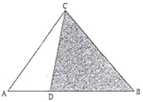 如图,在△ABC中,D是AB边上的点,且AD=
如图,在△ABC中,D是AB边上的点,且AD=| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|