题目内容
3.△ABC的三个顶点都在圆O上,$\overrightarrow{AO}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,且|$\overrightarrow{BC}$|=10,则圆O的面积为25π.分析 由向量的平行四边形法则可知BC为圆O的直径,代入面积公式即可.
解答 解:做圆O的直径AD,则$\overrightarrow{AD}$=2$\overrightarrow{AO}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$,∴四边形ABCD是平行四边形,
∵AD是直径,∴∠ACD=90°,∴四边形ABCD是矩形,∴BC=AD=10.即圆O的半径为5.
∴π×52=25π.
故答案为25π.
点评 本题考查了平面向量的线性运算和几何意义,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
11.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{FP}$=4$\overrightarrow{FQ}$,则QF等于3.
12.在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形,现有如图所示两种方案,则( )
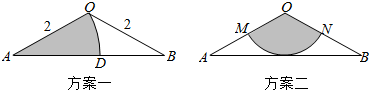

| A. | 方案一中扇形的周长更长 | B. | 方案二中扇形的周长更长 | ||
| C. | 方案一中扇形的面积更大 | D. | 方案二中扇形的面积更大 |
13.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则异面直线CM与DN所成的角的余弦值为( )
| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |