题目内容
18．函数f（x）=2x3-3x2-12x+5在[0，2]上的最大值和最小值分别是（ ）| A． | 12，-15 | B． | 5，-15 | C． | 12，-5 | D． | 5，-16 |
分析 对函数求导，利用导数求研究函数y=2x3-3x2-12x+5在[0，2]上的单调性，判断出最大值与最小值位置，代入算出结果．
解答 解：由题设知y'=6x2-6x-12，
令y'＞0，解得x＞2，或x＜-1，
故函数y=2x3-3x2-12x+5在[0，2]上减，
当x=0，y=5；当x=2，y=-15．
由此得函数y=2x3-3x2-12x+5在[0，2]上的最大值和最小值分别是5，-15；
故选：B．
点评 考查用导数研究函数的单调性求最值，本题是导数一章中最基本的题型．
练习册系列答案
阅读快车系列答案
相关题目
6．某省2016年高中数学学业水平测试的原始成绩采用百分制，发布成绩使用等级制，各等制划分标准如表所示：
同时认定A，B，C为合格，D为不合格．已知甲，乙两所学校学生的原始成绩均分布在[50，100]内，为了比较两校学生的成绩，分别抽取100名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出甲校的样本频率分布直方图如图1所示，乙校的样本中等级为C，D的所有数据茎叶图如图2所示．
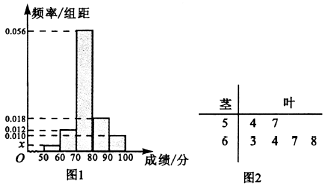
（1）求图中x的值，并根据样本数据比较甲乙两校的合格率；
（2）在乙校的样本中，从成绩等级为C的学生中随机抽取2名学生，从成绩等级为D的学生中随机抽取1名学生进行调研，求抽出的3名学生中恰有1名学生成绩在65分以上的概率．
| 分数 | [85，100] | [70，85） | [60，70） | [0，60） |
| 等级 | A等 | B等 | C等 | D等 |
（1）求图中x的值，并根据样本数据比较甲乙两校的合格率；
（2）在乙校的样本中，从成绩等级为C的学生中随机抽取2名学生，从成绩等级为D的学生中随机抽取1名学生进行调研，求抽出的3名学生中恰有1名学生成绩在65分以上的概率．
13．如果在犯错误的概率不超过0.05的前提下说事件A和B有关系，那么具体计算出的数据是（ ）
| A． | χ2≥3.841 | B． | χ2≤3.841 | C． | χ2≥6.635 | D． | χ2≤6.635 |
10．在锐角△ABC中，a=1，B=2A，则b的取值范围是（ ）
| A． | $（1，\sqrt{3}）$ | B． | $（\sqrt{2}，\sqrt{3}）$ | C． | $（\sqrt{2}，2）$ | D． | $（\sqrt{3}，2）$ |
7．已知数列{an}的各项均为正数，其前n项和为S，且na${\;}_{n+1}^{2}$=（n+1）a${\;}_{n}^{2}$+anan+1，a1=$\frac{π}{3}$，则tanSn的取值集合是（ ）
| A． | {0，$\sqrt{3}$} | B． | {0，$\sqrt{3}$，$\frac{\sqrt{3}}{3}$} | C． | {0，$\sqrt{3}$，$-\frac{\sqrt{3}}{3}$} | D． | {0，$\sqrt{3}$，-$\sqrt{3}$} |