题目内容
9.已知△ABC中,角C为直角,D是BC边上一点,M是AD上一点,且|CD|=1,∠DBM=∠DMB=∠CAB,则|MA|=2.分析 设∠DBM=θ,在△CDA中,由正弦定理可得$\frac{CD}{sin(\frac{π}{2}-2θ)}$=$\frac{AC}{sin2θ}$,在△AMB中,由正弦定理可得$\frac{MA}{sin(\frac{π}{2}-2θ)}$=$\frac{AB}{sin(π-θ)}$,继而可得$\frac{CD}{MA}$=$\frac{1}{2}$,问题得以解决
解答  解:设∠DBM=θ,则∠ADC=2θ,∠DAC=$\frac{π}{2}$-2θ,∠AMB=$\frac{π}{2}$-2θ,
解:设∠DBM=θ,则∠ADC=2θ,∠DAC=$\frac{π}{2}$-2θ,∠AMB=$\frac{π}{2}$-2θ,
在△CDA中,由正弦定理可得$\frac{CD}{sin(\frac{π}{2}-2θ)}$=$\frac{AC}{sin2θ}$,
在△AMB中,由正弦定理可得$\frac{MA}{sin(\frac{π}{2}-2θ)}$=$\frac{AB}{sin(π-θ)}$,
∴$\frac{CD}{MA}$=$\frac{ACsinθ}{ABsin2θ}$=$\frac{ACsinθ}{2ABsinθcosθ}$=$\frac{1}{2}$,
从而MA=2,
故答案为:2.
点评 本题考查了正弦定理的应用,关键是掌握应用的条件,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
17.已知四棱锥P-ABCD中,侧棱都相等,底面是边长为$2\sqrt{2}$的正方形,底面中心为O,以PO为直径的球经过侧棱中点,则该球的体积为( )
| A. | $\frac{{8\sqrt{2}}}{3}π$ | B. | $\frac{{4\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{32}{3}π$ |
14.函数y=log2(3x2-7x+2)的单调减区间为( )
| A. | ($\frac{7}{6}$,+∞) | B. | (-∞,$\frac{7}{6}$) | C. | (-∞,$\frac{1}{3}$) | D. | (2,+∞) |
18.函数f(x)=2x3-3x2-12x+5在[0,2]上的最大值和最小值分别是( )
| A. | 12,-15 | B. | 5,-15 | C. | 12,-5 | D. | 5,-16 |
19.已知在各棱长都为2的三棱锥A-BCD中,棱DA,DB,DC的中点分别为P,Q,R,则三棱锥Q-APR的体积为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{\sqrt{2}}{12}$ | D. | $\frac{\sqrt{2}}{16}$ |
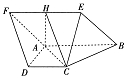 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.