题目内容
3.《九章算术》中有这样一段叙述:“今有良马与驽马发长安至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马.”则现有如下说法:①驽马第九日走了九十三里路;②良马五日共走了一千零九十五里路;③良马和驽马相遇时,良马走了二十一日.则错误的说法个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据题意,良马走的路程可以看成一个首项a1=193,公差d1=13的等差数列,记其前n项和为Sn,驽马走的路程可以看成一个首项b1=97,公差为d2=-0.5的等差数列,记其前n项和为Tn,由等差数列的通项公式以及其前n项和公式分析三个说法的正误,即可得答案.
解答 解:根据题意,良马走的路程可以看成一个首项a1=193,公差d1=13的等差数列,记其前n项和为Sn,
驽马走的路程可以看成一个首项b1=97,公差为d2=-0.5的等差数列,记其前n项和为Tn,
依次分析3个说法:
对于①、b9=b1+(9-1)×d2=93,故①正确;
对于②、S5=5a1+$\frac{5×4}{2}$×d1=5×193+10×13=1095;故②正确;
对于③、设第n天两马相遇,则有Sn+Tn≥6000,
即na1+$\frac{n(n-1)}{2}$d1+nb1+$\frac{n(n-1)}{2}$d2≥6000,变形可得5n2+227n-4800≥0,
分析可得n的最小值为16,
故两马相遇时,良马走了16日,故③错误;
3个说法中只有1个错误;
故选:B.
点评 本题考查等差数列的通项公式与求和公式,关键要熟悉等差数列的通项公式和前n项和公式.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
14.函数y=log2(3x2-7x+2)的单调减区间为( )
| A. | ($\frac{7}{6}$,+∞) | B. | (-∞,$\frac{7}{6}$) | C. | (-∞,$\frac{1}{3}$) | D. | (2,+∞) |
18.函数f(x)=2x3-3x2-12x+5在[0,2]上的最大值和最小值分别是( )
| A. | 12,-15 | B. | 5,-15 | C. | 12,-5 | D. | 5,-16 |
8.已知函数f(x)=x2-ax($\frac{1}{e}$≤x≤e,e为自然对数的底数)与g(x)=ex的图象上存在关于直线y=x对称的点,则实数a取值范围是( )
| A. | [1,e+$\frac{1}{e}$] | B. | [1,e-$\frac{1}{e}$] | C. | [e-$\frac{1}{e}$,e+$\frac{1}{e}$] | D. | [e-$\frac{1}{e}$,e] |
13.设函数f(x)的定义域为R,f(x)=$\left\{{\begin{array}{l}{x,0≤x<1}\\{{{(\frac{1}{3})}^x}-1,-1≤x<0}\end{array}}$且对任意的x∈R都有f(x+1)=f(x-1),若在区间[-1,5)上函数g(x)=f(x)-mx-m恰有4个不同零点,则实数m的取值范围是( )
| A. | $({0,\frac{1}{4}}]$ | B. | $({\frac{1}{4},\frac{1}{2}}]$ | C. | $[{\frac{1}{4},\frac{1}{2}})$ | D. | $({0,\frac{1}{2}})$ |
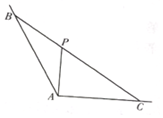 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.