题目内容
在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n为何值时,Sn取得最大值,并求出它的最大值.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由题意和等差数列的性质可得数列的前12项为正数,第13项为0,从第14项开始为负值,易得当n=12或13时,Sn取得最大值,由可得公差d,代入求和公式可得.
解答:
解:∵等差数列{an}中S10=S15,
∴S15-S10=a11+a12+a13+a14+a15=5a13=0,
∴a13=0,
∴数列的前12项为正数,第13项为0,从第14项开始为负值,
∴当n=12或13时,Sn取得最大值,
又公差d=
=-
,
∴S12=12×20+
(-
)=130
∴Sn的最大值为130
∴S15-S10=a11+a12+a13+a14+a15=5a13=0,
∴a13=0,
∴数列的前12项为正数,第13项为0,从第14项开始为负值,
∴当n=12或13时,Sn取得最大值,
又公差d=
| a13-a1 |
| 13-1 |
| 5 |
| 3 |
∴S12=12×20+
| 12×11 |
| 2 |
| 5 |
| 3 |
∴Sn的最大值为130
点评:本题考查等差数列的求和公式,从数列项的正负变化入手是解决问题的关键,属基础题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
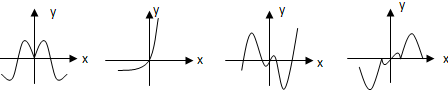
则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
已知f(x)=(4a-3)x+b-2a,x∈[0,1],若f(x)≤2恒成立,则t=a+b的最大值为( )
A、
| ||
| B、4 | ||
C、
| ||
D、
|