题目内容
 在给定坐标系中作出函数f(x)=x2-4|x|-2的图象,并根据图象写出函数的单调增区间,单调减区间及不等式f(x)>0的解集.
在给定坐标系中作出函数f(x)=x2-4|x|-2的图象,并根据图象写出函数的单调增区间,单调减区间及不等式f(x)>0的解集.
解:f(x)= ,其图象如图.
,其图象如图.
f(x)是偶函数,图象关于y轴对称.
(2)函数的单增区间是[-2,0],[2,+∞) 单减区间是(-∞,-2],[0,2]
图象与x轴交点坐标是(0, ),(0,
),(0, )
)
不等式f(x)>0的解集是(-∞, )
) .
.
分析:将函数解析式化简,去掉绝对值符号,化为分段函数,再作图.由图象易写出单调区间.不等式f(x)>0的解集为图象在x轴上方时对应的x取值范围.
点评:本题考查函数的图象,单调区间,分段函数知识,数形结合的思想.若函数有多个单增(减)区间,在写时逐一写出,中间用逗号隔开.
 ,其图象如图.
,其图象如图.f(x)是偶函数,图象关于y轴对称.

(2)函数的单增区间是[-2,0],[2,+∞) 单减区间是(-∞,-2],[0,2]
图象与x轴交点坐标是(0,
 ),(0,
),(0, )
)不等式f(x)>0的解集是(-∞,
 )
) .
.分析:将函数解析式化简,去掉绝对值符号,化为分段函数,再作图.由图象易写出单调区间.不等式f(x)>0的解集为图象在x轴上方时对应的x取值范围.
点评:本题考查函数的图象,单调区间,分段函数知识,数形结合的思想.若函数有多个单增(减)区间,在写时逐一写出,中间用逗号隔开.

练习册系列答案
相关题目
函数f(x)=cos(2x-
),x∈R.
(Ⅰ)先完成下列表格,然后在给定坐标系中作出函数f(x)在[0,π]上的图象;
(Ⅱ)若f(
+
)=
,-
<α<0,求sin(2α-
)的值.
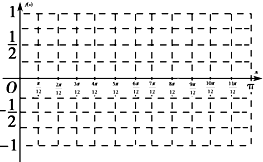
| π |
| 3 |
(Ⅰ)先完成下列表格,然后在给定坐标系中作出函数f(x)在[0,π]上的图象;
(Ⅱ)若f(
| α |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
2x-
|
-
|
0 |
|
π |
|
|||||||||
| x | 0 |
|
|
|
π | |||||||||
| f(x) |
|
-1 |

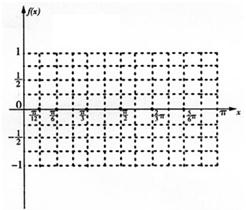 设x∈R,函数f(x)=cos(ωx+?)(ω>0,
设x∈R,函数f(x)=cos(ωx+?)(ω>0,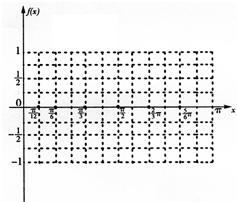 设x∈R,函数
设x∈R,函数 在给定坐标系中作出函数f(x)=x2-4|x|-2的图象,并根据图象写出函数的单调增区间,单调减区间及不等式f(x)>0的解集.
在给定坐标系中作出函数f(x)=x2-4|x|-2的图象,并根据图象写出函数的单调增区间,单调减区间及不等式f(x)>0的解集.