Question

函数f（x）=cos（2x-

π

3

），x∈R．
（1）先完成下列表格，然后在给定坐标系中作出函数f（x）在上[0，π]的图象；

2x- π 3	- π 3	0	π 2	π	3π 2	5π 3
x	0	π 6	5π 12	2 3 π	11π 12	π
f（x）	12			-1

（2）求函数f（x）=cos（2x-

π

3

），x∈R的单调增区间．

Answer 1

分析：（1）根据函数表达式，直接求出函数值完成表格，结合点的坐标           给定坐标系中作出函数f（x）在上[0，π]的图象；
（2）通过余弦函数的单调增区间，直接求解函数f（x）=cos（2x-

π

3

），x∈R的单调增区间．

解答：解：（Ⅰ）完成表格如图：

2x- π 3	- π 3	0	π 2	π	3π 2	5π 3
x	0	π 6	5π 12	2 3 π	11π 12	π
f（x）	12	1	0	-1	0	1 2

图象如图：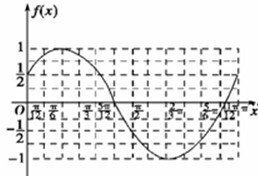
（2）由-π+2kπ≤2x-

π

3

≤2kπ，k∈Z      （8分）
得-

2π

3

+2kπ≤2x≤

π

3

+2kπ，k∈Z．
  -

π

3

+kπ≤x≤

π

6

+kπ，k∈Z           （10分）
所以函数f（x）=cos（2x-

π

3

）的单调增区间为[-

π

3

+kπ，

π

6

+kπ]，k∈Z．   12分）

点评：本题考查三角函数的图象的画法以及函数的单调性的求法，考查计算能力以及作图能力．