题目内容
 设x∈R,函数f(x)=cos(ωx+?)(ω>0,-
设x∈R,函数f(x)=cos(ωx+?)(ω>0,-| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
(Ⅰ)求ω和?的值;
(Ⅱ)在给定坐标系中作出函数f(x)在[0,π]上的图象;
(Ⅲ)若f(x)>
| ||
| 2 |
分析:(I)由周期求ω,由特殊点求φ;
(II)明确函数f(x),借用五点法,先列表,再画图;
(III)利用余弦函数的单调性解之即可.
(II)明确函数f(x),借用五点法,先列表,再画图;
(III)利用余弦函数的单调性解之即可.
解答:解:(I)周期T=
=π,∴ω=2,
∵f(
)=cos(2×
+φ)=cos(
+φ)=-sinφ=
,
且-
<φ<0,∴φ=-
.
(II)知f(x)=cos(2x-
),则列表如下:
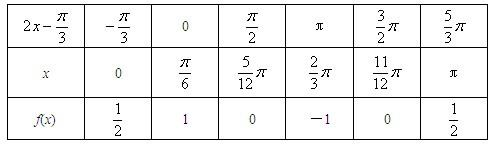
图象如图:
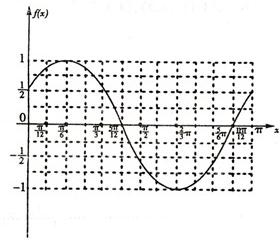
(III)∵cos(2x-
)>
,
∴2kπ-
<2x-
<2kπ+
解得kπ+
<x<kπ+
,k∈Z,
∴x的范围是{x|kπ+
<x<kπ+
π,k∈Z}.
| 2π |
| ω |
∵f(
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
且-
| π |
| 2 |
| π |
| 3 |
(II)知f(x)=cos(2x-
| π |
| 3 |

图象如图:

(III)∵cos(2x-
| π |
| 3 |
| ||
| 2 |
∴2kπ-
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
解得kπ+
| π |
| 24 |
| 7 |
| 24 |
∴x的范围是{x|kπ+
| π |
| 24 |
| 7 |
| 24 |
点评:本题考查三角函数中ω、φ的确定方法、五点法作图及三角函数的单调性.

练习册系列答案
相关题目