题目内容
函数f(x)=cos(2x-| π |
| 3 |
(Ⅰ)先完成下列表格,然后在给定坐标系中作出函数f(x)在[0,π]上的图象;
(Ⅱ)若f(
| α |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
2x-
|
-
|
0 |
|
π |
|
|||||||||
| x | 0 |
|
|
|
π | |||||||||
| f(x) |
|
-1 |
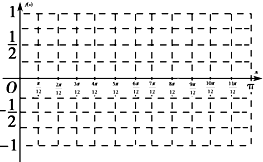
分析:(Ⅰ)根据三角函数的数值关系先完成下列表格,然后在给定坐标系中作出函数f(x)在[0,π]上的图象;
(Ⅱ)根据三角公式求出sin2α和cos2α的值,利用两角和差的正弦公式进行求解即可.
(Ⅱ)根据三角公式求出sin2α和cos2α的值,利用两角和差的正弦公式进行求解即可.
解答: 解:(Ⅰ)完成表格:
解:(Ⅰ)完成表格:
图象如图:
(Ⅱ)f(
+
)=cosα=
,
∵-
<α<0,
∴sinα=-
=-
,
∴sin2α=2sinαcosα=2×
×(-
)=-
,
cos2α=2cos2α-1=-
,
∴sin(2α-
)=sin2αcos
-cos2αsin
=-
•
-(-
)•
=-
.
 解:(Ⅰ)完成表格:
解:(Ⅰ)完成表格:2x-
|
-
|
0 |
|
π |
|
| ||||||||||
| x | 0 |
|
|
|
|
π | ||||||||||
| f(x) |
|
1 | 0 | -1 | 0 |
|
(Ⅱ)f(
| α |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
∵-
| π |
| 2 |
∴sinα=-
| 1-cos2α |
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
cos2α=2cos2α-1=-
| 7 |
| 25 |
∴sin(2α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=-
| 24 |
| 25 |
| ||
| 2 |
| 7 |
| 25 |
| ||
| 2 |
=-
17
| ||
| 50 |
点评:本题主要考查三角函数的图象和性质,利用两角和与差的正弦公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=cos(2x+
)是( )
| π |
| 2 |
| A、最小正周期为π的偶函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的奇函数 | ||
D、最小正周期为
|