Question

设x∈R，函数f(x)=Acos(ωx+φ)(A，ω＞0，-

π

2

＜φ＜0)的最小正周期为π，最大值是1，其图象经过点M(

π

4

，

3

2

)．
（Ⅰ） 求f（x）的解析式；    
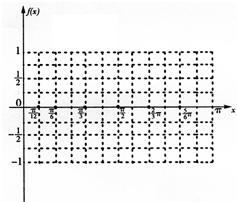
（Ⅱ）在给定坐标系中作出函数f（x）在[0，π]上的图象．

Answer 1

分析：（I）由已知中函数f(x)=Acos(ωx+φ)(A，ω＞0，-

π

2

＜φ＜0)的最小正周期为π，最大值是1，我们易求出A、ω的值，又由图象经过点M(

π

4

，

3

2

)．代入求出φ值，即可求出f（x）的解析式；    
（Ⅱ）根据（I）所求的函数的解析式，利用五点法，我们易得到函数f（x）在[0，π]上的图象．

解答：解：（I）∵函数f(x)=Acos(ωx+φ)(A，ω＞0，-

π

2

＜φ＜0)的最小正周期为π，最大值是1，
∴A=1，ω=2
则f（x）=cos（2x+?）
又∵其图象经过点M(

π

4

，

3

2

)．
∴

3

2

=cos（

π

2

+?）=-sin?
解得?=-

π

3

∴f（x）=cos（2x-

π

3

）
（II）函数f（x）在[0，π]上的图象如下图所示：

点评：本题考查的知识点是五点法作函数y=Asin（ωx+φ）的图象及五点法作函数y=Asin（ωx+φ）的解析式的求法，其中熟练掌握A，ω，φ与函数最值，周期，向左平移量等之间的关系，是解答本题的关键．