题目内容
17.已知F1,F2是双曲线的两个焦点,Q是双曲线上除顶点外的任意一点.从某一焦点引∠F1QF2的平分线的垂线,垂足为P.则P的轨迹为( )| A. | 抛物线 | B. | 椭圆 | C. | 圆 | D. | 双曲线 |
分析 利用已知条件判断出△MQF1为等腰三角形,利用双曲线的定义及等量代换得到MF2=2a,利用三角形的中位线得到OP=a,利用圆的定义判断出点的轨迹.
解答 解:设O为F1F2的中点
延长F1P交QF2于M,连接OP
据题意知△MQF1为等腰三角形
所以QF1=QM
∵|QF1-QF2|=2a
∴|QM-QF2|=2a
即MF2=2a
∵OP为△F1F2M的中位线
∴OP=a
故点P的轨迹为以O为圆心,以a为半径的圆.
故选:C
点评 本题考查双曲线的定义、原点定义及等量代换的数学方法、三角形的中位线性质.

练习册系列答案
相关题目
5.为迎接2013年全运会的到来,组委会在大连市招募了100名志愿者,其中男、女志愿者各50名,调查是否喜欢运动得到如下统计数据.由于一些原因,丢失了其中四个数据,目前知道这四个数据c,a,b,d恰好成递增的等差数列.
(Ⅰ)将联表中数据补充完整,并判断是否有95%的把握认为性别与运动有关?
(Ⅱ) 调查中显示喜欢运动的男志愿者中有10%懂得医疗救护,而喜欢运动的女志愿者中有40%懂得医疗救护,从中抽取2人组成医疗救护小组,则这个医疗救护小组恰好是一男一女的概率有多大?
附:χ2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜欢运动 | 不喜欢运动 | 总计 | |
| 男 | a | b | 50 |
| 女 | c | d | 50 |
| 总计 | 30 | 70 | 100 |
(Ⅱ) 调查中显示喜欢运动的男志愿者中有10%懂得医疗救护,而喜欢运动的女志愿者中有40%懂得医疗救护,从中抽取2人组成医疗救护小组,则这个医疗救护小组恰好是一男一女的概率有多大?
附:χ2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(χ2≥k) | 0.05 | 0.001 |
| k | 3.841 | 6.635 |
9.下列关于算法的说法中,正确的是( )
| A. | 算法是某个问题的解决过程 | B. | 算法执行后可以不产生确定的结果 | ||
| C. | 解决某类问题的算法不是唯一的 | D. | 算法可以无限的操作下去不停止 |
6.已知函数g(x)=$\sqrt{2{x^2}-3x+1}$,则函数g(x)的定义域为( )
| A. | (-∞,$\frac{1}{2}$]∪[2,+∞) | B. | [$\frac{1}{2}$,1] | C. | (-∞,$\frac{1}{2}$]∪[1,+∞) | D. | (-∞,-1]∪[$\frac{1}{2}$,+∞) |
7.定义运算(a,b)?(c,d)=ac-bd,则符合条件(z,1-2i)?(-1,1+i)=0的复数z的所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
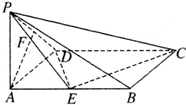 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.