题目内容
斜率为k(k≠0)的两条直线分别切函数f(x)=x3+(t-1)x2-1的图象于A、B两点,若直线AB的方程为y=2x-1,则t+k的值为( )
| A、8 | B、7 | C、6 | D、5 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:可设A(x1,y1),B(x2,y2),求出函数f(x)的导数,可得x1,x2为3x2+2(t-1)x-k=0的两根,运用韦达定理,再由直线AB方程和函数f(x)联立,消去y,得到x的方程,再由韦达定理,解方程可得k=6,t=1,即可得到结论.
解答:
解:可设A(x1,y1),B(x2,y2),
函数f(x)=x3+(t-1)x2-1的导数为f′(x)=3x2+2(t-1)x,
则x1,x2为3x2+2(t-1)x-k=0的两根,
即有x1+x2=
,x1x2=-
,(k≠0),
又直线AB的方程为y=2x-1,
代入y=x3+(t-1)x2-1,可得2x=x3+(t-1)x2,
由于切点的横坐标不为0,则x2+(t-1)x-2=0,
则有x1+x2=1-t,x1x2=-2,
由-2=-
,1-t=
,解得k=6,t=1,
即有k+t=7.
故选B.
函数f(x)=x3+(t-1)x2-1的导数为f′(x)=3x2+2(t-1)x,
则x1,x2为3x2+2(t-1)x-k=0的两根,
即有x1+x2=
| 2(1-t) |
| 3 |
| k |
| 3 |
又直线AB的方程为y=2x-1,
代入y=x3+(t-1)x2-1,可得2x=x3+(t-1)x2,
由于切点的横坐标不为0,则x2+(t-1)x-2=0,
则有x1+x2=1-t,x1x2=-2,
由-2=-
| k |
| 3 |
| 2(1-t) |
| 3 |
即有k+t=7.
故选B.
点评:本题考查导数的几何意义:曲线在该点处切线的斜率,运用韦达定理是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
命题“对任意实数x∈[1,2],关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是( )
| A、a≥4 | B、a≤4 |
| C、a≥3 | D、a≤3 |
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
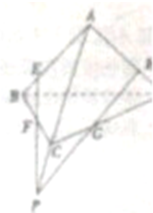

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |
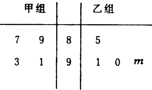 如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示.
如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示.