题目内容
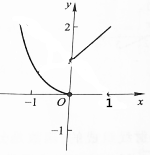
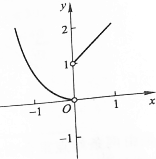
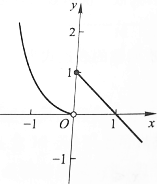
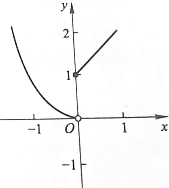
4.由曲线y=x2和曲线y=$\sqrt{1-(x-1)^{2}}$所围成的图形的面积为( )| A. | $\frac{π}{4}$-$\frac{1}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{2}$+1 |
分析 绘制出积分区域,利用定积分的性质,求得阴影的面积可以转化为$\frac{1}{4}$π•12-${∫}_{0}^{1}{x}^{2}dx$.
解答  解:由图形可知S=$\frac{1}{4}$π•12-${∫}_{0}^{1}{x}^{2}dx$=$\frac{π}{4}$-$\frac{1}{3}$,
解:由图形可知S=$\frac{1}{4}$π•12-${∫}_{0}^{1}{x}^{2}dx$=$\frac{π}{4}$-$\frac{1}{3}$,
故答案选:A.
点评 本题考查定积分求阴影部分的面积,属于基础题.

练习册系列答案
相关题目
14.“?x>0,使a+x<b”是“a<b”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.动点P(x,y)到点O(0,0)的距离是到点A(3,-3)的距离的$\sqrt{2}$倍,则点P的轨迹方程是( )
| A. | x2-12y+y2+12y+36=0 | B. | x2+6x+y2-12y+36=0 | ||
| C. | x2+12x+y2-12y+36=0 | D. | x2-6x+y2+6y+18=0 |
14.已知(1+px)(1-x+x2)8的展开式中x4项的系数是42,则p的值是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |