题目内容
已知O为△ABC的外心,AB=2a,AC=
(a>0),∠BAC=120°,若
=x
+y
(x,y为实数),则x+4y的最小值为 .
| 2 |
| a |
| AO |
| AB |
| AC |
考点:基本不等式,平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据几何图形求解出O点的坐标,先求出
,
的坐标,再由
=x
+y
(x,y为实数)运用向量的坐标相等求解出x,y的值,得出x+4y=
×(
+4a2)+
运用基本不等式求解即可得出最小值.
| AB |
| AC |
| AO |
| AB |
| AC |
| 1 |
| 3 |
| 1 |
| a2 |
| 10 |
| 3 |
解答:
解:∵O为△ABC的外心,AB=2a,AC=
(a>0),∠BAC=120°
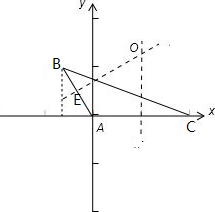
∴建立坐标系如图:过O作AB的垂直平分线,垂足为E,
A(0,0),C(
,0),B(-a,
a),E(-
,
),O(,
,m)
∵∠BAC=120,
∴
=
,
化简多得出:m=
+
,
∴O(
,
+
)
∴
=(
,0),
=(-a,
a),
=(
,
+
),
∵
=x
+y
(x,y为实数),
∴
解得:x=
+
,2y=
+
a2,
∴x+4y=
×(
+4a2)+
≥
×4+
=
x+4y的最小值为:
,
故答案为:
| 2 |
| a |
∴建立坐标系如图:过O作AB的垂直平分线,垂足为E,
A(0,0),C(
| 2 |
| a |
| 3 |
| a |
| 2 |
| ||
| 2 |
| 1 |
| a |

∵∠BAC=120,
∴
m-
| ||||
|
| ||
| 3 |
化简多得出:m=
| ||
| 3a |
2
| ||
| 3 |
∴O(
| 1 |
| a |
| ||
| 3a |
2
| ||
| 3 |
∴
| AC |
| 2 |
| a |
| AB |
| 3 |
| AO |
| 1 |
| a |
| ||
| 3a |
2
| ||
| 3 |
∵
| AO |
| AB |
| AC |
∴
|
| 1 |
| 3a2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
∴x+4y=
| 1 |
| 3 |
| 1 |
| a2 |
| 10 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
| 14 |
| 3 |
x+4y的最小值为:
| 14 |
| 3 |
故答案为:
| 14 |
| 3 |
点评:本题考查了平面向量的坐标运算,结合基本不等式求解,属于中档题,关键是准确求解向量的坐标.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数y=xa+b,x∈(0,+∞)是增函数,则( )
| A、a>0,b是任意实数 |
| B、a<0,b是任意实数 |
| C、b>0,a是任意实数 |
| D、b<0,a是任意实数 |
已知命题p:若x>10,则x>1,那么命题p的逆否命题为( )
| A、若x≤10,则x≤1 |
| B、若x>1,则x>10 |
| C、若x≤1,则x≤10 |
| D、若x>10,则x≤1 |