题目内容
已知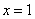 是函数
是函数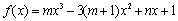 的一个极值点,其中
的一个极值点,其中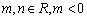 ,
,
(I)求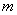 与
与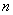 的关系式;(II)求
的关系式;(II)求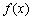 的单调区间; (III)当
的单调区间; (III)当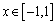 时,函数
时,函数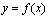 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3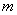 ,求
,求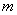 的取值范围.
的取值范围.
解:(I) ,因为
,因为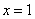 是函数
是函数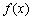 的一个极值点,所以
的一个极值点,所以 ,即
,即 ,所以
,所以
(II)由(I)知, =
=
当 时,有
时,有 ,当
,当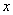 变化时,
变化时, 与
与 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
|
| 0 |
| 0 |
|
|
| 调调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
故由上表知,当 时,
时,
 在
在 单调递减,在
单调递减,在 单调递增,在
单调递增,在 上单调递减.
上单调递减.
(III)由已知得 ,即
,即
又 所以
所以 即
即 ①
①
设,其函数开口向上,由题意知①式恒成立,
所以
 解之得
解之得 又
又 所以
所以
即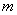 的取值范围为
的取值范围为

练习册系列答案
相关题目
从某大学中随机抽取8名女大学生, 其身高和体重数据如表所示.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高/cm | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重/kg | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
已知该大学某女大学生身高为165.25cm, 则预报其体重合理值为 kg.








 中,角
中,角 为钝角,且
为钝角,且 ,则
,则 的取值范围是 .
的取值范围是 .  满足
满足 ,则
,则 的最小值为 .
的最小值为 . 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点 到直线
到直线 和直线
和直线 的距离之和的最小值是( )
的距离之和的最小值是( ) D.
D.
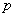 :实数
:实数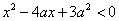 ,其中
,其中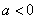 ,命题
,命题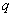 :实数
:实数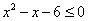 或
或 ,且
,且 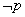 是
是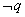 的必要不充分条件,求
的必要不充分条件,求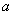 的取值范围.
的取值范围. 的渐近线方程为
的渐近线方程为 ,则
,则 的值为( )
的值为( ) 在区间[-2,2]上的值域是_
在区间[-2,2]上的值域是_