题目内容
已知sinβ+cosβ=
,β∈(0,π)
(1)求tanβ的值;
(2)求sin2β的值;
(3)你能根据所给的条件,自己构造出一些求值问题吗?
| 1 |
| 5 |
(1)求tanβ的值;
(2)求sin2β的值;
(3)你能根据所给的条件,自己构造出一些求值问题吗?
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)将已知等式两边平方,利用同角三角函数间基本关系化简,求出sinβcosβ的值,进而求出sinβ-cosβ的值,联立求出sinβ与cosβ的值,即可确定出tanβ的值;
(2)原式利用二倍角的正弦函数公式化简,将各自的值代入计算即可求出值;
(3)求出cos2β的值.
(2)原式利用二倍角的正弦函数公式化简,将各自的值代入计算即可求出值;
(3)求出cos2β的值.
解答:
解:(1)将已知等式sinβ+cosβ=
①,两边平方得:(sinβ+cosβ)2=1+2sinβcosβ=
,即2sinβcosβ=-
<0,
∴(sinβ-cosβ)2=1-2sinβcosβ=
,
∵β∈(0,π),
∴sinβ>0,cosβ<0,即sinβ-cosβ>0,
∴sinβ-cosβ=
②,
联立①②得:sinβ=
,cosβ=-
,
则tanβ=
=-
;
(2)∵sinβ=
,cosβ=-
,
∴sin2β=2sinβcosβ=2×
×(-
)=-
;
(3)∵sinβ=
,cosβ=-
,
∴cos2β=cos2β-sin2β=
-
=-
.
| 1 |
| 5 |
| 1 |
| 25 |
| 24 |
| 25 |
∴(sinβ-cosβ)2=1-2sinβcosβ=
| 49 |
| 25 |
∵β∈(0,π),
∴sinβ>0,cosβ<0,即sinβ-cosβ>0,
∴sinβ-cosβ=
| 7 |
| 5 |
联立①②得:sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
则tanβ=
| sinβ |
| cosβ |
| 4 |
| 3 |
(2)∵sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
∴sin2β=2sinβcosβ=2×
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
(3)∵sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
∴cos2β=cos2β-sin2β=
| 9 |
| 25 |
| 16 |
| 25 |
| 7 |
| 25 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
z=
,则|z|=( )
| 5+12i |
| 3+4i |
A、
| ||
B、
| ||
C、
| ||
D、
|
各大学在高考录取时采取专业志愿优先的录取原则.一考生从某大学所给的7个专业中,选择3个作为自己的第一、二、三专业志愿,其中甲、乙两个专业不能同时兼报,则该考生不同的填报专业志愿的方法有( )
| A、210种 | B、180种 |
| C、120种 | D、95种 |
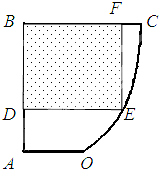 某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.
某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.