题目内容
设函数f(x)=|2x-a|+2a.
(1)若不等式f(x)≤6解集为{x|-6≤x≤4},求实数a的值;
(2)在(1)的条件下,若不等式f(x)≤kx-5的解集非空,求实数k取值范围?
(1)若不等式f(x)≤6解集为{x|-6≤x≤4},求实数a的值;
(2)在(1)的条件下,若不等式f(x)≤kx-5的解集非空,求实数k取值范围?
考点:绝对值不等式的解法
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:(1)运用绝对值不等式的解法,结合方程的解的概念可得a的方程,解得即可;
(2)不等式f(x)≤kx-5,即为|2x+2|≤kx-1,作出函数y=|2x+2|,y=kx-1的图象,通过直线绕着点(0,-1)旋转,观察即可得到满足条件的可得范围.
(2)不等式f(x)≤kx-5,即为|2x+2|≤kx-1,作出函数y=|2x+2|,y=kx-1的图象,通过直线绕着点(0,-1)旋转,观察即可得到满足条件的可得范围.
解答:
 解:(1)因为f(x)≤6即为|2x-a|≤6-2a,
解:(1)因为f(x)≤6即为|2x-a|≤6-2a,
即2a-6≤2x-a≤6-2a
即
a-3≤x≤3-
.
因为其解集为{x|-6≤x≤4},
所以
a-3=-6且3-
=4,
解得:a=-2;
(2)由(1)知f(x)=|2x+2|-4,
所以不等式f(x)≤kx-5,即为|2x+2|≤kx-1,
作出函数y=|2x+2|,y=kx-1的图象,
由图象可得k≤-1或k>2.
则有k的取值范围为(-∞,-]∪(2,+∞).
 解:(1)因为f(x)≤6即为|2x-a|≤6-2a,
解:(1)因为f(x)≤6即为|2x-a|≤6-2a,即2a-6≤2x-a≤6-2a
即
| 3 |
| 2 |
| a |
| 2 |
因为其解集为{x|-6≤x≤4},
所以
| 3 |
| 2 |
| a |
| 2 |
解得:a=-2;
(2)由(1)知f(x)=|2x+2|-4,
所以不等式f(x)≤kx-5,即为|2x+2|≤kx-1,
作出函数y=|2x+2|,y=kx-1的图象,
由图象可得k≤-1或k>2.
则有k的取值范围为(-∞,-]∪(2,+∞).
点评:本题考查绝对值不等式的解法,考查数形结合的思想方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知A(0,-5),B(0,5),|PA|-|PB|=2a,当a=3或5时,P点的轨迹为( )
| A、双曲线和一条直线 |
| B、双曲线和两条直线 |
| C、双曲线的一支和一条直线 |
| D、双曲线的一支和一条射线 |
集合A={(x,y)|x+y=10,x∈N*,y∈N*}的元素个数为( )
| A、8 | B、9 | C、10 | D、100 |
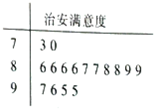 某网站用“10分制”调查一社区人们的治安满意度,现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某网站用“10分制”调查一社区人们的治安满意度,现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):