题目内容
13.已知双曲线C:${x^2}-\frac{y^2}{{{3^{\;}}}}=1$,A、B是双曲线上关于原点对称的两点,M是双曲线上异于A、B的一点,直线MA、MB的斜率分别记为k1,k2,且k1∈[-3,-1],则k2的取值范围是[-3,-1].分析 设出点A,点M,点B的坐标,求出斜率,将点A,B的坐标代入方程,两式相减,再结合k1∈[-3,-1],即可求得结论.
解答 解:由题意,设A(x1,y1),M(x2,y2),则B(-x1,-y1)
∴k1•k2=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$•$\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}$=$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$,
∵${{x}_{1}}^{2}$-$\frac{{{y}_{1}}^{2}}{3}$=1,${{x}_{2}}^{2}$-$\frac{{{y}_{2}}^{2}}{3}$=1,
∴两式相减可得$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=3
∵k1∈[-3,-1],∴k2∈[-3,-1].
故答案为:[-3,-1].
点评 本题考查双曲线的方程,考查双曲线的几何性质,考查直线的斜率公式和点差法的运用,属于中档题.

练习册系列答案
相关题目
7.已知二面角α-l-β为60°,如果平面角α内一点A到平面β的距离为$\sqrt{3}$,那么A到棱的距离为( )
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
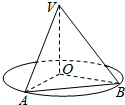
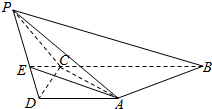 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,AD=CD=1,BC=2,又PC=1,∠PCB=120°,PB⊥CD,点E在棱PD上,且PE=2ED.
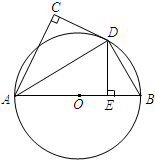 如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.
如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.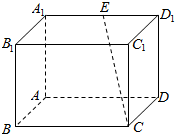 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.