Question

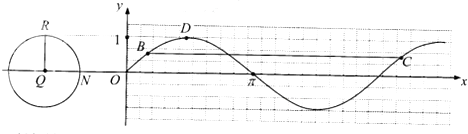
已知f（x）=Asin（ωx+φ）（ω＞0，-

π

2

＜φ＜

π

2

）图象的一部分如图所示．
（Ⅰ）写出A，ω，φ的值；
（Ⅱ）已知g（x）=f（x+

π

6

），求出g（x）的单调增区间．
（Ⅲ）若D是f（x）图象上一个最高点，则用单位圆上的圆心角（弧度数）表示x_D为x_D=∠NQR（0≤∠NQR≤

π

2

）．
现有f（x）图象上两个点B，C（BC∥x轴）对应的横坐标分别为x_B，x_C，请在左边单位圆上作出x_B，x_C对应的正弦线MP，并用单位圆上圆心角（弧度数）表示x_B，x_C的大小．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象

专题：计算题,三角函数的图像与性质

分析：（Ⅰ）由图象观察即可求得A，ω，φ的值．
（Ⅱ）由-

π

2

+2kπ≤x+

π

6

≤

π

2

+2kπ，k∈Z可解得g（x）的单调增区间．
（Ⅲ）延长线段CB交单位圆Q于点P（如图），过P作PM⊥x轴于点M，则MP为x_B，x_C对应的正弦线，即可得解．

解答： 解：（Ⅰ）A=1，ω=1，φ=0；…3分
（Ⅱ）g（x）=f（x+

π

6

）=sin（x+

π

6

）…4分
当g（x）为增函数时，-

π

2

+2kπ≤x+

π

6

≤

π

2

+2kπ，k∈Z…5分
即有-

2π

3

+2kπ≤x≤

π

3

+2kπ，k∈Z…7分
∴g（x）的单调增区间是：[-

2π

3

+2kπ，

π

3

+2kπ]，k∈Z…8分
（Ⅲ）延长线段CB交单位圆Q于点P（如图），过P作PM⊥x轴于点M，则MP为x_B，x_C对应的正弦线…10分
∵x_B∈（0，

π

2

），∴x_B=∠MQP（0≤∠MQP≤

π

2

）…12分
∵x_C∈（2π，

5π

2

），∴x_C=2π+=∠MQP（0≤∠MQP≤

π

2

）…14分
注：未注明0≤∠MQP≤

π

2

不扣分．

点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，正弦函数的图象和性质，属于基础题．