题目内容
12.已知a>0且a≠1,(2a)m=a,(3a)m=2a,求证:($\frac{3}{2}$)mn=2n.分析 由$\frac{(3a)^{m}}{(2a)^{m}}$=$\frac{2a}{a}=2$,得到($\frac{3}{2}$)m=2,由此能证明($\frac{3}{2}$)mn=2n.
解答 证明:∵a>0且a≠1,(2a)m=a,(3a)m=2a,
∴$\frac{(3a)^{m}}{(2a)^{m}}$=$\frac{2a}{a}=2$,
∴($\frac{3}{2}$)m=2,
∴($\frac{3}{2}$)mn=[($\frac{3}{2}$)m]n=2n.
∴($\frac{3}{2}$)mn=2n.
点评 本题考查有理数指数幂等式成立的证明,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数y=sin2x+cos2x如何平移可以得到函数y=sin2x-cos2x图象( )
| A. | 向左平移$\frac{π}{2}$ | B. | 向右平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
7.△ABC中,A=45°,B=30°,a=10,则b=( )
| A. | 5$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{6}$ | D. | 5$\sqrt{6}$ |
17.函数f(x)=x3-3x2+1是减函数的单调区间为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,0) | D. | (0,2) |
1.已知实数x,y满足约束条件$\left\{{\begin{array}{l}{x+y+1≥0}\\{{x^2}+{y^2}≤4}\\{xy≥0}\end{array}}\right.$,则z=2x+y的取值范围是( )
| A. | $[-2,2\sqrt{5}]$ | B. | [-2,0] | C. | $[-2\sqrt{5},2]$ | D. | $[\frac{{2\sqrt{5}}}{5},1]$ |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.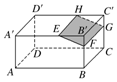 如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.
如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.