题目内容
15. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.(Ⅰ)若E为PB的中点,证明:AE∥平面PCD;
(Ⅱ)求证:AB⊥PC
(Ⅲ)若F为PD的中点,求二面角F-AC-D的平面角的大小.
分析 (Ⅰ)取PC中的H,连结EH,证明四边形EHDA为平行四边形,得到AE∥DH,即可得AE∥面PDC,
(Ⅱ)取BC中的G,连结AG,证明AB⊥AC,AB⊥PA,得到AB⊥面PAC,即可得到AB⊥AC.
(Ⅲ)取AD的中的M,连结FM,则FM∥PA,由PA⊥平面ABCD,则FM⊥平面ABCD,过点M,作MN⊥AC,连结FN,则二面角F-AC-D的平面角为∠FNM,在直角三角形FNM中求解,
解答 解:(Ⅰ)取PC中的H,连结EH,HD,因为E为PB的中的,所以EH∥BC,EH=$\frac{1}{2}BC$,
由AD∥BC,且AD=$\frac{1}{2}BC$,得EH∥AD,且EH=AD,∴四边形EHDA为平行四边形.
∴AE∥DH,AE?面PDC,DH?面PDC,∴AE∥面PDC,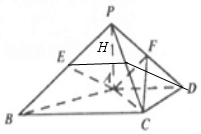
(Ⅱ)取BC中的G,连结AG,则AD∥GC,AD=GC,∴四边形AGCD为平行四边形∴AG⊥BC,
又AG=BG=GC=2$\sqrt{2}$,∴∠ABC=∠ACD=45°,故AB⊥AC,
又PA⊥平面ABCD,∴AB⊥PA,且AC∩PA=A,∴AB⊥面PAC,∴AB⊥AC.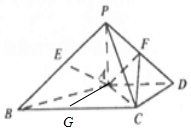
(Ⅲ)取AD的中的M,连结FM,则FM∥PA,由PA⊥平面ABCD,则FM⊥平面ABCD,
过点M,作MN⊥AC,连结FN,则FN⊥AC,
∴二面角F-AC-D的平面角为∠FNM,在直角三角形FNM中,$PM=\frac{1}{2}PA=1,MN=1$,
$tan∠FNM=\frac{FM}{MN}=1$,∴二面角F-AC-D的平面角的大小为$\frac{π}{4}$.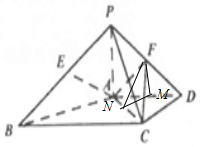
点评 本题考查了空间线面平行、线线垂直、几何法求二面角,关键是弄清线线、线面、面面位置关系,合理准确添加辅助线,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
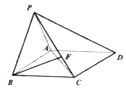 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.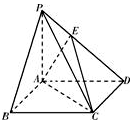 四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$
四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$