题目内容
1.三角形ABC中,cosBcosC=1-sinBsinC,三角形ABC的形状为等腰三角形.分析 利用两角差的余弦函数公式可求cos(B-C)=1,结合B-C的范围,利用余弦函数的图象和性质即可得解B-C=0,从而得解.
解答 解:∵cosBcosC=1-sinBsinC,
∴cosBcosC+sinBsinC=cos(B-C)=1,
∵B∈(0,π),C∈(0,π),可得:-π<B-C<π,
∴解得:B-C=0,即B=C.
∴可得三角形ABC的形状为:等腰三角形.
故答案为:等腰三角形.
点评 本题主要考查了两角差的余弦函数公式,余弦函数的图象和性质的应用,属于基本知识的考查.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
12.已知a=2-sin1,b=-$\frac{π}{6}$+sin$\frac{π}{12}$,c=-$\frac{π}{4}$+sin$\frac{π}{8}$,则( )
| A. | b>c>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
11.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点F与抛物线y2=2px(p>0)的焦点重合,且在第一象限的交点为M,MF直于x轴,则双曲线的离心率是( )
| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$+2 |
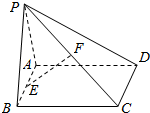 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E,F分别是AB,PC的中点.