题目内容
8.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1(x≥0)}\\{2x(x<0)}\end{array}\right.$若f(a)=10,那么a=3.分析 当a≥0时,f(a)=a2+1=10;当a<0时,2a=10.由此能求出a.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1(x≥0)}\\{2x(x<0)}\end{array}\right.$,f(a)=10,
∴当a≥0时,f(a)=a2+1=10,解得a=3或a=-3(舍);
当a<0时,2a=10,解得a=5,不成立.
综上,a=3.
故答案为:3.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
19.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.设集合A={x|2x-3≥1},集合$B=\left\{{x|y=\frac{sinx}{{\sqrt{5-x}}}}\right\}$,则A∩B=( )
| A. | (2,5) | B. | [2,5] | C. | (2,5] | D. | [2,5) |
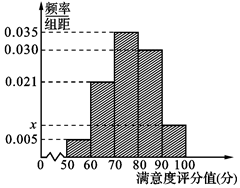 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照 分成5组,制成如图所示频率分直方图.