题目内容
16.已知等差数列{an}满足a3=7,a5+a7=26,若${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$(n∈N*),则数列{bn}的前10项和S10=$\frac{10}{69}$.分析 利用等差中项及a5+a7=26可知a6=13,进而可知公差d=$\frac{{a}_{6}-{a}_{3}}{6-3}$=2,从而an=2n+1,进而利用裂项相消法计算即得结论.
解答 解:因为数列{an}是等差数列,
所以2a6=a5+a7=26,即a6=13,
又因为a3=7,
所以公差d=$\frac{{a}_{6}-{a}_{3}}{6-3}$=2,
所以an=a3+(n-3)d=2n+1,
所以${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$=$\frac{1}{2n+1}$•$\frac{1}{2n+3}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$)(n∈N*),
所以数列{bn}的前10项和S10=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{21}$-$\frac{1}{23}$)=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{23}$)=$\frac{10}{69}$,
故答案为:$\frac{10}{69}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法求和,注意解题方法的积累,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
6.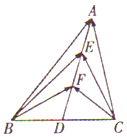 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
 如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )
如图.在△ABC中,D是BC的中点,E、F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是( )| A. | 4 | B. | 8 | C. | $\frac{7}{8}$ | D. | $\frac{3}{4}$ |
7.已知$sinα=\frac{{\sqrt{10}}}{10}$,$sin(α-β)=-\frac{{\sqrt{5}}}{5}$,$α,β∈(0,\frac{π}{2})$,则β=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
11.在△ABC中,已知sin(A+B)=2sinAcosB,那么△ABC一定是( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
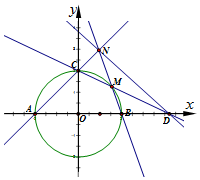 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.