题目内容
17.已知不等式组$\left\{\begin{array}{l}2x-y+3≥0\\ x≤1\\ x-2y≤0\end{array}\right.$表示的平面区域为D,若函数y=|x|+m的图象上存在区域D上的点,则实数m的最小值为( )| A. | -4 | B. | -3 | C. | -1 | D. | $-\frac{1}{2}$ |
分析 作出可行域,由y=|x|的图象特点,平移图象可得.
解答 解:作出不等式组$\left\{\begin{array}{l}2x-y+3≥0\\ x≤1\\ x-2y≤0\end{array}\right.$表示的平面区域D(如图示):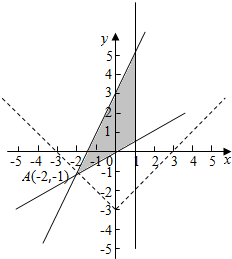 ,
,
由$\left\{\begin{array}{l}{2x-y+3=0}\\{x-2y=0}\end{array}\right.$,解得:A(-2,-1),
函数y=|x|的图象为直线y=x保留x轴上方的并把x轴下方的上翻得到,
其图象为关于y轴对称的折线(图中红色虚线),
沿y轴上下平移y=|x|的图象,当经过点A时m取最小值,
∴-1=2+m,解得:m=-3,
故选:B.
点评 本题考查简单线性规划,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
20.在△ABC中,角A、B、C所对边分别为a、b、c且满足asinB=b,则当$\sqrt{2}$sinB+sinC取得最大值时,cosB的值为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
8.设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1,F2,P是椭圆上的点.若PF1⊥F1F2,∠F1PF2=60°,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.已知函数f(x)满足f(1)=0,且f(x)在R上的导数满足f′(x)+1<0,则不等式f(x2)<-x2+1的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (1,+∞) | C. | (-∞,1) | D. | (-1,1 ) |
9.已知向量$\overrightarrow{a}$=(x1,y1,z1),$\overrightarrow{b}$=(x2,y2,z2),$\overrightarrow{a}$≠$\overrightarrow{b}$,设|$\overrightarrow{a}-\overrightarrow{b}$|=k,则|$\overrightarrow{a}-\overrightarrow{b}$与单位向量$\overrightarrow{i}$=(1,0,0)夹角的余弦值为( )
| A. | $\frac{{x}_{1}-{x}_{2}}{k}$ | B. | $\frac{{x}_{2}-{x}_{1}}{k}$ | C. | $\frac{|{x}_{1}-{x}_{2}|}{k}$ | D. | ±$\frac{{x}_{1}-{x}_{2}}{k}$ |