题目内容
6.利用定积分的定义计算∫${\;}_{1}^{2}$(1+x)dx的值.分析 根据定积分的定义,∫${\;}_{1}^{2}$(1+x)dx表示直线y=x+1,与x=1,x=2所围成的图形的面积,求出面积即可.
解答  解:∫${\;}_{1}^{2}$(1+x)dx表示直线y=x+1,与x=1,x=2所围成的图形的面积,如图所示:
解:∫${\;}_{1}^{2}$(1+x)dx表示直线y=x+1,与x=1,x=2所围成的图形的面积,如图所示:
其面积为S=$\frac{1}{2}$BC•(AB+CD)=$\frac{1}{2}$×1×(2+3)=$\frac{5}{2}$,
∴∫${\;}_{1}^{2}$(1+x)dx=$\frac{5}{2}$
点评 本题考查了定积分定义,关键是求出直线y=x+1,与x=1,x=2所围成的图形的面积,是基础的计算题.

练习册系列答案
相关题目
17.已知不等式组$\left\{\begin{array}{l}2x-y+3≥0\\ x≤1\\ x-2y≤0\end{array}\right.$表示的平面区域为D,若函数y=|x|+m的图象上存在区域D上的点,则实数m的最小值为( )
| A. | -4 | B. | -3 | C. | -1 | D. | $-\frac{1}{2}$ |
1.圆心在曲线y=$\frac{1}{x}$(x>0)上,与直线2x+y+1=0相切且面积最小的圆的方程为( )
| A. | (x-1)2+(y-2)2=5 | B. | (x-1)2+(y-1)2=5 | C. | (x-1)2+(y-2)2=25 | D. | (x-1)2+(y-1)2=25 |
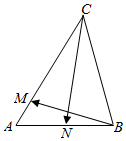 在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.
在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.