题目内容
16．求证：函数f（x）=$\sqrt{x}$+a在（0，+∞）上是增函数．分析 根据函数单调性的定义证明即可．
解答 证明：设?x1，x2满足x1＞x2＞0，
则f（x1）-f（x2）=$\sqrt{{x}_{1}}$-$\sqrt{{x}_{2}}$=$\frac{（\sqrt{{x}_{1}}-\sqrt{{x}_{2}}）（\sqrt{{x}_{1}}+\sqrt{{x}_{2}}）}{\sqrt{{x}_{1}}+\sqrt{{x}_{2}}}$=$\frac{{x}_{1}{-x}_{2}}{\sqrt{{x}_{1}}+\sqrt{{x}_{2}}}$，
∵$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$＞0，x1-x2＞0，∴f（x1）-f（x2）＞0，
∴f（x）=$\sqrt{x}$+a在（0，+∞）上是增函数．
点评 本题考查了根据函数的单调性的定义证明函数的单调性问题，是一道基础题．
练习册系列答案
相关题目
6．已知集合A={x|x＜0}，B={x|（x+2）（x-3）≤0}，则A∩B=（ ）
| A． | {x|-3≤x＜0} | B． | {x|-3＜x＜-2} | C． | {x|-2≤x＜0} | D． | {x|x≤3} |
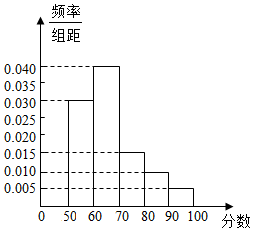某校举行的数学知识竞赛中，将参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．
1．不等式x2+x＜$\frac{a}{b}$+$\frac{b}{a}$ 对任意a，b∈（0，+∞）恒成立，则实数x的取值范围是（ ）
| A． | （-2，0） | B． | （-∞，-2）∪（1，+∞） | C． | （-2，1） | D． | （-∞，-4）∪（2，+∞） |