题目内容
13.(a2+b2)2n展开式的项数是2n+1.分析 根据二项式定理,把二项式(a2+b2)2n展开,即得展开式的项数是2n+1.
故答案为:2n+1.
解答 解:二项式(a2+b2)2n=${C}_{2n}^{0}$(a2)2n+${C}_{2n}^{1}$•(a2)2n-1•b2+…+${C}_{2n}^{2n-1}$•a2•(b2)2n-1+${C}_{2n}^{2n}$•(b2)2n,
∴(a2+b2)2n展开式的项数是2n+1.
故答案为:2n+1.
点评 本题考查了二项式展开式的项数应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.不等式x2+x<$\frac{a}{b}$+$\frac{b}{a}$ 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-4)∪(2,+∞) |
18.化简$\sqrt{9{x^2}-6x+1}-{({\sqrt{3x-5}})^2}$,结果是( )
| A. | 6x-6 | B. | -6x+6 | C. | -4 | D. | 4 |
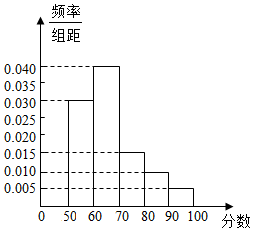 某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.