题目内容

14．已知数列{an}是等比数列，且a3=1，a5a6a7=8，则9=4．

分析 由已知条件利用等比数列的通项公式列出方程组，求出首项与公比，由此能求出结果．

解答 解：∵数列{an}是等比数列，且a3=1，a5a6a7=8，
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=1}\\{{{a}_{1}}^{3}{q}^{15}=8}\end{array}\right.$，
解得${a}_{1}=\frac{1}{\root{3}{4}}$，q=$\root{3}{2}$，
∴${a}_{9}={a}_{1}{q}^{8}$=$\frac{1}{\root{3}{4}}×（\root{3}{2}）$8=4．
故答案为：4．

点评 本题考查等比数列的第9项的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

练习册系列答案
相关题目
8．若函数 f（x）=ae-x-ex为奇函数，则f（x-1）＜e-$\frac{1}{e}$的解集为（　　）
A．（-∞，0）B．（-∞，2）C．（2，+∞）D．（0，+∞）
5．已知函数$f（x）=\frac{sinx}{{sin（x+\frac{π}{2}）}}$，则（　　）
A．f（x）的最小正周期是2πB．f（x）相邻对称中心相距$\frac{π}{2}$个单位
C．f（x）相邻渐近线相距2π个单位D．f（x）既是奇函数又是增函数
2．已知数列{an}满足a1=q（q≠0），对任意m、p∈N*都有am+p=am•ap．从数列{an}中取出部分项，并将它们按原来顺序组成一个数列，称之为数列{an}的一个子数列．
（Ⅰ）求a4；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）证明：当q＞0且q≠1时，数列{an}不存在无穷等差子数列．
9．已知集合A={x|x2+4x+3≥0}，B={x|2x＜1}，则A∩B=（　　）
A．[-3，-1]B．（-∞，-3]∪[-1，0）C．（-∞，-3）∪（-1，0]D．（-∞，0）
19．若函数f（x）=sin（2x+φ）（-π＜φ＜0）为偶函数，则函数f（x）在区间$[0，\frac{π}{4}]$上的取值范围是（　　）
A．[-1，0]B．$[-\frac{{\sqrt{2}}}{2}，0]$C．$[0，\frac{{\sqrt{2}}}{2}]$D．[0，1]
6．已知集合A={x|x＜0}，B={x|（x+2）（x-3）≤0}，则A∩B=（　　）
A．{x|-3≤x＜0}B．{x|-3＜x＜-2}C．{x|-2≤x＜0}D．{x|x≤3}
3．在数列{an}中，${a_1}=1，\frac{a_n}{{{a_{n-1}}}}=\frac{{1-\sqrt{a_n}}}{{1+\sqrt{{a_{n-1}}}}}（n＞1）$．
（Ⅰ）求证：数列$\left\{{\frac{1}{{\sqrt{a_n}}}}\right\}$是等差数列；
（Ⅱ）令${b_n}=lg\frac{{1-\sqrt{{a_{n+1}}}}}{{1+\sqrt{a_n}}}$，求数列{bn}的前数列n项和Sn．
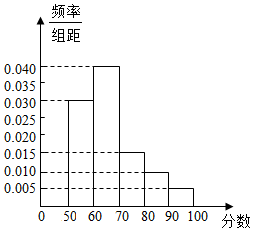4．某校举行的数学知识竞赛中，将参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．
（1）求成绩在50-70分的频率是多少；
（2）求这次参赛学生的总人数是多少；
（3）求这次数学竞赛成绩的平均分的近似值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网