题目内容
13.已知$f(x)={sin^2}(2x-\frac{π}{4})-2t•sin(2x-\frac{π}{4})+{t^2}-6t+1(x∈[\frac{π}{24},\frac{π}{2}])$其最小值为g(t).(1)若t=1,求$f({\frac{π}{8}})$的值;
(2)求g(t)的表达式;
(3)当$-\frac{1}{2}≤t≤1$时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
分析 (1)若t=1,代入计算求$f({\frac{π}{8}})$的值;
(2)分类讨论,求g(t)的表达式;
(3)令h(t)=g(t)-kt,欲使g(t)=kt有一个实根,则只需$\left\{{\begin{array}{l}{h(-\frac{1}{2})≤0}\\{h(1)≥0}\end{array}}\right.$或$\left\{{\begin{array}{l}{h(-\frac{1}{2})≥0}\\{h(1)≤0}\end{array}}\right.$,即可求实数k的取值范围.
解答 解:(1)t=1,$f({\frac{π}{8}})$=1-6+1=-4 …(3分)
(2)因为$x∈[\frac{π}{24},\frac{π}{2}]$,所以$2x-\frac{π}{4}∈[-\frac{π}{6},\frac{3π}{4}]$,
所以$sin(2x-\frac{π}{4})∈[-\frac{1}{2},1]$…(5分)
$f(x)={[sin(2x-\frac{π}{4})-t]^2}-6t+1$($x∈[\frac{π}{24},\frac{π}{2}]$)
当$t<-\frac{1}{2}$时,则当sin(2x-$\frac{π}{4}$)=-$\frac{1}{2}$时,${[f(x)]_{min}}={t^2}-5t+\frac{5}{4}$…(6分)
当-$\frac{1}{2}$≤t≤1时,则当sin(2x-$\frac{π}{4}$)=t时,f(x)min=-6t+1 …(7分)
当t>1时,则当sin(2x-$\frac{π}{4}$)=1时,${[f(x)]_{min}}={t^2}-8t+2$…(8分)
故g(t)=$\left\{\begin{array}{l}{{t}^{2}-5t+\frac{5}{4},t<-\frac{1}{2}}\\{-6t+1,-\frac{1}{2}≤t≤1}\\{{t}^{2}-8t+2,t>1}\end{array}\right.$ …(9分)
(3)当$-\frac{1}{2}≤t≤1$时,g(t)=-6t+1,令h(t)=g(t)-kt
欲使g(t)=kt有一个实根,则只需$\left\{{\begin{array}{l}{h(-\frac{1}{2})≤0}\\{h(1)≥0}\end{array}}\right.$或$\left\{{\begin{array}{l}{h(-\frac{1}{2})≥0}\\{h(1)≤0}\end{array}}\right.$
解得k≤-8或k≥-5. …(12分)
点评 本题考查函数的最值,考查三角函数知识的运用,考查学生分析解决问题的能力,属于中档题.

| A. | (-∞,$\frac{\sqrt{e}}{e}$-8] | B. | [$\frac{\sqrt{e}}{e}$-8,+∞) | C. | [$\sqrt{2}$,e) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{e}{2}$] |
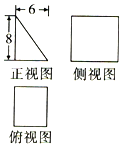
| A. | 96 | B. | 144 | C. | 192 | D. | 240 |