题目内容
已知非零向量列{an}满足:a1=(1,1),且an=(xn,yn)= (xn-1-yn-1,xn-1+yn-1) (n>1,n∈N),令|an|=bn.
(xn-1-yn-1,xn-1+yn-1) (n>1,n∈N),令|an|=bn.(Ⅰ)证明:数列{bn}是等比数列,并求{bn}的通项公式;
(Ⅱ)对n∈N*,设cn=bnlog2bn,试问是否存在正整数m,使得cm<cm+1?若存在,请求出m的最小值,若不存在,请说明理由.
【答案】分析:(I)要证数列bn为等比数列,利用了等比数列的定义,由题意找数列bn和相邻项bn+1的比为常数,并利用等比数列通项公式求其通项
(II)由题意应先求出cn,由题意在建立cn与cn+1之间的不等关系,利用作差的等价转化思想求解关于m不等式,再利用m的范围逼出m的最小值
解答:(I)证明:bn=|an|=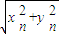 ,
,
bn+1=|an+1|=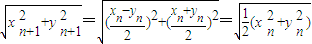 ,
,
∴ (常数),
(常数),
∴{bn}是等比数列,其中b1=|a1|=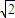 ,公比
,公比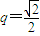 ,
,
∴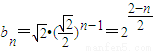 .(5分)
.(5分)
(II)∵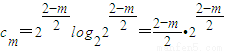 ,
,
∴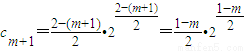 ,
,
于是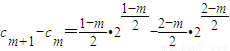 =
=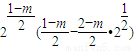 ,(8分)
,(8分)
∵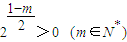 ,
,
∴要使cm+1>cm,只须使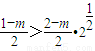 ,即
,即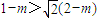 ,
,
解得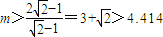 .(11分)
.(11分)
∵m是正整数,
∴m≥5,m∈N*,
∴m的最小值为5.(12分)
点评:(I)此问重在考查等比数列的定义及等比数列的通项公式
(II)此处重在考查了对数的运算性质进而准确求出cn的通项,之后又考查了建立m的不等式及解不等式
(II)由题意应先求出cn,由题意在建立cn与cn+1之间的不等关系,利用作差的等价转化思想求解关于m不等式,再利用m的范围逼出m的最小值
解答:(I)证明:bn=|an|=
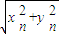 ,
,bn+1=|an+1|=
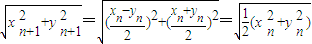 ,
,∴
 (常数),
(常数),∴{bn}是等比数列,其中b1=|a1|=
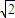 ,公比
,公比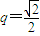 ,
,∴
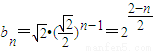 .(5分)
.(5分)(II)∵
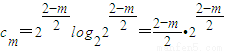 ,
,∴
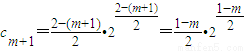 ,
,于是
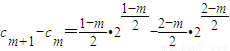 =
=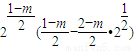 ,(8分)
,(8分)∵
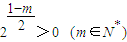 ,
,∴要使cm+1>cm,只须使
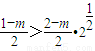 ,即
,即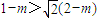 ,
,解得
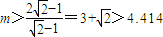 .(11分)
.(11分)∵m是正整数,
∴m≥5,m∈N*,
∴m的最小值为5.(12分)
点评:(I)此问重在考查等比数列的定义及等比数列的通项公式
(II)此处重在考查了对数的运算性质进而准确求出cn的通项,之后又考查了建立m的不等式及解不等式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目