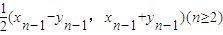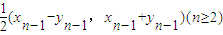Question

已知一非零向量列{a_n}满足：a₁=（1，2），an=(xn，yn)=(-

1

2

yn-1，

1

2

xn-1)(n≥2)
（1）证明：{|a_n|}是等比数列；
（2）求向量a_n-1与a_n的夹角θ（n≥2）；
（3）把向量a₁，a₂，…，a_n…中所有与a₁共线的向量按原来的前后顺序排成一列，记为b₁，b₂，…，b_n，…，其中b₁=a₁，若

OBn

=b1+b2+…+bn=(Tn，Sn)（O是坐标原点），求S_n

Answer 1

分析：（1）用等比数列的定义证明：先求|an|=

x 2 n + y 2 n

=

1

2

x 2 n-1 + y 2 n-1

=

1

2

|an-1|(n≥2)，通过

|an|

|an-1|

=

1

2

．(n≥2)符合等比数列的定义可证，但要注意明确首项和公比．
（2）根据向量的夹角公式来求，先求数量积，再分别求模，代入公式求解．
（3）由（2）知，a₁∥a₃∥a₅∥奇数项共线，则b_n=a_2n-1．由an=(xn，yn)=(-

1

2

yn-1•

1

2

xn-1)(n∈N*，n≥2)，得an=-

1

4

an-2，从而有bn=-

1

4

bn-1=(-

1

4

)n-1再由等比数列前n项和公式求解．

解答：解：（1）证明：|an|=

x 2 n + y 2 n

=

1

2

x 2 n-1 + y 2 n-1

=

1

2

|an-1|(n≥2)，
∴

|an|

|an-1|

=

1

2

．(n≥2)
又|a1|=

5

，∴{|a_n|}是首项为

5

．公比为

1

2

的等比数列．（4分）
（2）∵an-1•an=(xn-1•yn-1)•(-

1

2

yn-1•

1

2

xn-1)=0，∴a_n-1与a_n的夹角θ=90°（6分）
（3）∴由（2）知，a₁∥a₃∥a₅∥．即b_n=a_2n-1．
由an=(xn，yn)=(-

1

2

yn-1•

1

2

xn-1)(n∈N*，n≥2)，得xn=-

1

2

yn-1，yn=-

1

2

xn-1．
∴xn=-

1

2

yn-1=-

1

2

(

1

2

xn-2)=-

1

4

xn-2•yn=

1

2

xn-1=

1

2

(-

1

2

yn-2)=-

1

4

yn-2，
∴an=-

1

4

an-2，∴bn=-

1

4

bn-1=(-

1

4

)n-1b1=(-

1

4

)n-1(1，2)，
∴Sn=2[1+(-

1

4

)+(-

1

4

)2++(-

1

4

)n-1]=

8

5

[1-(-

1

4

)n]（12分）

点评：本题主要考查知识间的转化与应用，涉及到数列的判断与证明，通项公式及前n项和公式的灵活运用．