题目内容
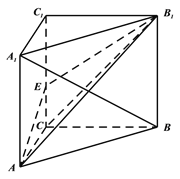
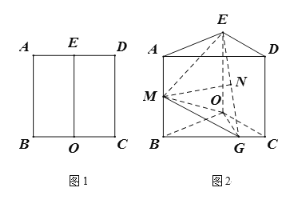
【题目】请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得
四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm2
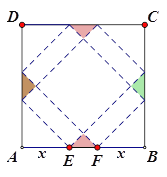
（1）若广告商要求包装盒侧面积S（cm
）最大，试问x应取何值？
（2）若广告商要求包装盒容积V（cm
）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值。
【答案】（1）x=15cm （2）
【解析】
试题（1）先设包装盒的高为
，底面边长为
，写出
，
与
的关系式，并注明的取值范围，再利用侧面积公式表示出包装盒侧面积
关于的函数解析式，最后求出何时它取得最大值即可；
（2）利用体积公式表示出包装盒容积
关于的函数解析式，利用导数知识求出何时它取得的最大值即可．
设包装盒的高为，底面边长为
由已知得
（1）∵
∴当
时，取得最大值
（2）根据题意有
∴
。
由
得，
(舍)或
。
∴当
时
；当
时
∴当
时取得极大值，也是最大值，此时包装盒的高与底面边长的比值为
即包装盒的高与底面边长的比值为．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】为了了解市民对开设传统文化课的态度，教育机构随机抽取了
位市民进行了解，发现支持开展的占
，在抽取的男性市民
人中持支持态度的为
人.
（1）完成
列联表，并判断是否有
的把握认为性别与支持与否有关？
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
（2）为了进一步征求对开展传统文化的意见和建议，从抽取的位市民中对不支持的按照分层抽样的方法抽取
位市民，并从抽取的人中再随机选取
人进行座谈，求选取的人恰好为
男女的概率.
附：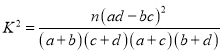
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某大学为了调查该校学生性别与身高的关系，对该校1000名学生按照
的比例进行抽样调查，得到身高频数分布表如下：
男生身高频率分布表
男生身高 （单位：厘米） |
|
|
|
|
|
|
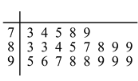
频数 | 7 | 10 | 19 | 18 | 4 | 2 |
女生身高频数分布表
女生身高 （单位：厘米） |
|
|
|
|
|
|
频数 | 3 | 10 | 15 | 6 | 3 | 3 |
（1）估计这1000名学生中女生的人数；
（2）估计这1000名学生中身高在
的概率；
（3）在样本中，从身高在
的女生中任取2名女生进行调查，求这2名学生身高在
的概率.（身高单位：厘米）
