题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )过点
)过点![]() 与
与![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过椭圆![]() 的右焦点
的右焦点![]() ,且倾斜角为
,且倾斜角为![]() 的直线
的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 、
、![]() 两点,对于椭圆
两点,对于椭圆![]() 上任一点
上任一点![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)把已知点的坐标代入椭圆方程,得到关于![]() ,
,![]() 的方程组,求解可得
的方程组,求解可得![]() ,
,![]() 的值,则椭圆的方程可求;
的值,则椭圆的方程可求;
(2)由(1)知,![]() ,
,![]() ,由题意可知
,由题意可知![]() 的方程,与椭圆方程联立,化为关于
的方程,与椭圆方程联立,化为关于![]() 的一元二次方程,由
的一元二次方程,由![]() ,
,![]() ,
,![]() 在椭圆上及根与系数的关系可得
在椭圆上及根与系数的关系可得![]() ,再由基本不等式求最值.
,再由基本不等式求最值.
解:(1)∵椭圆过点![]() 与
与![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,∴椭圆的方程为
,∴椭圆的方程为![]() .
.
(2)由(1)知![]() ,由题意可知
,由题意可知![]() 的方程为
的方程为![]() ,①
,①
椭圆的方程可化为![]() ,②
,②
将①代入②消去![]() ,得
,得![]() ,③
,③
设![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,
,
设![]() ,由
,由![]() 得
得![]() ,
,
∴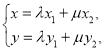 又点
又点![]() 在椭圆上,
在椭圆上,
∴![]()
![]()
![]() ,④
,④
又![]() ,
,![]() 在椭圆上,故有
在椭圆上,故有![]() ,
,![]() ,⑤
,⑤
而![]()
![]()
![]() ,⑥
,⑥
将⑤⑥代入④可得![]() ,
,
∵![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时取“=”,则
时取“=”,则![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目