题目内容
11.若角α的终边过点(-4,-3),则cosα=$-\frac{4}{5}$;$tan({α+\frac{π}{4}})$7.分析 角α的终边过点P(-4,-3),可得|OP|=5.利用三角函数的定义、和差公式即可得出.
解答 解:∵角α的终边过点P(-4,-3),
∴|OP|=$\sqrt{(-4)^{2}+(-3)^{2}}$=5.
∴sinα=$\frac{-3}{5}$,cosα=$\frac{-4}{5}$.
tanα=$\frac{-3}{-4}$=$\frac{3}{4}$.
$tan({α+\frac{π}{4}})$=$\frac{tanα+1}{1-tanα}$=$\frac{\frac{3}{4}+1}{1-\frac{3}{4}}$=7.
故答案分别为:$\frac{-4}{5}$,7.
点评 本题考查了三角函数的定义、和差公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.角α 终边经过点(-sin20°,cos20°),则角α的最小正角是( )
| A. | 110°? | B. | 160°? | C. | 290°? | D. | 340°? |
20.设全集U={1,2,3,4,5},集合A={1,2,4},B={4,5},则集合A∩(∁UB)=( )
| A. | {1,2} | B. | {3,5} | C. | {4} | D. | {5} |
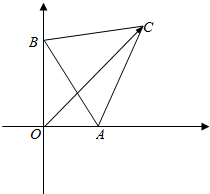 如图,线段AB长度为2,点A,B分别在x轴的正半轴和y轴的正半轴上滑动,以线段AB为一边,在第一象限内作等边三角形,O为坐标原点,则$\overrightarrow{OC}$•$\overrightarrow{OB}$的取值范围是[0,3].
如图,线段AB长度为2,点A,B分别在x轴的正半轴和y轴的正半轴上滑动,以线段AB为一边,在第一象限内作等边三角形,O为坐标原点,则$\overrightarrow{OC}$•$\overrightarrow{OB}$的取值范围是[0,3].