题目内容
甲、乙两人独自破译一个密码,他们能独立译出密码的概率分别为 和
和 .
.
①求甲、乙两人都不能译出密码的概率;
②假设有3个与甲同样能力的人一起独自破译该密码(甲、乙两人均不参加),求译出该密码的人数ξ概率分布和数学期望.
解:①由题意知本题是一个相互独立事件同时发生的概率,
设“甲、乙两人均不能译出密码”为事件A,
则P(A)=(1- )(1-
)(1- )=
)= 即甲、乙两人均不能译出密码的概率是
即甲、乙两人均不能译出密码的概率是 ;
;
②译出该密码的人数ξ的可能取值有0、1、2、3,且
P(ξ=0)= =
= ;P(ξ=1)=
;P(ξ=1)= =
= ;P(ξ=2)=
;P(ξ=2)= =
= ;P(ξ=3)=
;P(ξ=3)= =
=
∴ξ的概率分布列为
∴Eξ=0× +1×
+1× +2×
+2× +3×
+3× =1.5.
=1.5.
分析:①由题意知本题是一个相互独立事件同时发生的概率,求出对立事件的概率,即可求得结论;
②确定译出该密码的人数ξ的可能取值,求出相应的概率,可得ξ的概率分布和数学期望.
点评:本题考查概率知识的运用,考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值,求出相应的概率.
设“甲、乙两人均不能译出密码”为事件A,
则P(A)=(1-
 )(1-
)(1- )=
)= 即甲、乙两人均不能译出密码的概率是
即甲、乙两人均不能译出密码的概率是 ;
;②译出该密码的人数ξ的可能取值有0、1、2、3,且
P(ξ=0)=
 =
= ;P(ξ=1)=
;P(ξ=1)= =
= ;P(ξ=2)=
;P(ξ=2)= =
= ;P(ξ=3)=
;P(ξ=3)= =
=
∴ξ的概率分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =1.5.
=1.5.分析:①由题意知本题是一个相互独立事件同时发生的概率,求出对立事件的概率,即可求得结论;
②确定译出该密码的人数ξ的可能取值,求出相应的概率,可得ξ的概率分布和数学期望.
点评:本题考查概率知识的运用,考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ”是“a,b,c成等差数列”的________条件.
”是“a,b,c成等差数列”的________条件.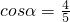 ,
, ,0<α<π,且
,0<α<π,且 ,则sin(α+β)的值为
,则sin(α+β)的值为


 是实数,则a=
是实数,则a=
 ,假设汽锤每次击打能将桩打入的长度为前一次击打打入长度的
,假设汽锤每次击打能将桩打入的长度为前一次击打打入长度的 ,桩受击打n次后恰好全部进入地里,那么n=________.
,桩受击打n次后恰好全部进入地里,那么n=________.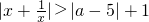 恒成立,则实数a的取值范围是 ________.
恒成立,则实数a的取值范围是 ________.