题目内容
?x∈R,且x≠0.不等式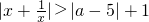 恒成立,则实数a的取值范围是 ________.
恒成立,则实数a的取值范围是 ________.
4<a<6
分析:不等式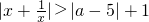 对于一切非零实数x均成立,可以先求出
对于一切非零实数x均成立,可以先求出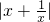 的最小值,然后利用|a-5|+1小于这个最小值即可求解a的取值范围.
的最小值,然后利用|a-5|+1小于这个最小值即可求解a的取值范围.
解答:当x>0时,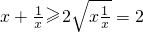 ;
;
当x<0时, .
.
从而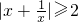 恒成立,
恒成立,
所以不等式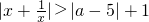 对于一切非零实数x均成立,
对于一切非零实数x均成立,
可转化为|a-5|+1<2,即|a-5|<1
即-1<a-5<1所以4<a<6.
故答案为:4<a<6.
点评:应用基本不等式求最值,一定注意一正、二定、三相等;对于恒成立的问题一般转化为求函数的最值,体现了转化和分类讨论的数学思想方法.属中档题.
分析:不等式
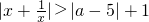 对于一切非零实数x均成立,可以先求出
对于一切非零实数x均成立,可以先求出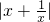 的最小值,然后利用|a-5|+1小于这个最小值即可求解a的取值范围.
的最小值,然后利用|a-5|+1小于这个最小值即可求解a的取值范围.解答:当x>0时,
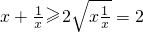 ;
;当x<0时,
 .
.从而
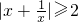 恒成立,
恒成立,所以不等式
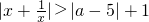 对于一切非零实数x均成立,
对于一切非零实数x均成立,可转化为|a-5|+1<2,即|a-5|<1
即-1<a-5<1所以4<a<6.
故答案为:4<a<6.
点评:应用基本不等式求最值,一定注意一正、二定、三相等;对于恒成立的问题一般转化为求函数的最值,体现了转化和分类讨论的数学思想方法.属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目