题目内容
已知：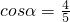
，
，0＜α＜π，且
，则sin（α+β）的值为
- A.1
- B.-1
- C.
- D.
C
分析：由条件结合角的范围求出sinα 和 sinβ 的值，再由两角和差的正弦公式 求出sin（α+β）=sinαcosβ+cosαsinβ的值．
解答：∵已知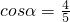：，，0＜α＜π，且，
则 sinα=
，sinβ=-
．
故sin（α+β）=sinαcosβ+cosαsinβ=
+
=，
故选C．
点评：本题主要考查两角和差的正弦公式的应用，同角三角函数的基本关系，注意三角函数值的符号，属于中档题．
分析：由条件结合角的范围求出sinα 和 sinβ 的值，再由两角和差的正弦公式 求出sin（α+β）=sinαcosβ+cosαsinβ的值．
解答：∵已知：
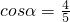，，0＜α＜π，且，则 sinα=
，sinβ=-．故sin（α+β）=sinαcosβ+cosαsinβ=
+=，故选C．
点评：本题主要考查两角和差的正弦公式的应用，同角三角函数的基本关系，注意三角函数值的符号，属于中档题．
练习册系列答案
相关题目
已知集合A={x|0≤x≤4}，则下列对应关系中不能构成定义域和值域都是A的函数的是（ ）
| A、y=4-x | ||
B、y=
| ||
| C、y=|x| | ||
D、y=
|