题目内容
12.若实数x、y满足|x|≤y≤1,则x2+y2+2x的最小值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
分析 画出约束条件表示的可行域,通过表达式的几何意义,求出表达式的最小值.
解答  解:x,y满足|x|≤y≤1,表示的可行域如图:
解:x,y满足|x|≤y≤1,表示的可行域如图:
x2+y2+2x=(x+1)2+y2-1它的几何意义是可行域内的点到(-1,0)的距离的平方减去1.
显然D(-1,0)到直线x+y=0的距离最小,
最小值为:$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
所求表达式的最小值为:$\frac{1}{2}-1$=$-\frac{1}{2}$,
故选:B.
点评 本题考查线性规划的简单应用,注意约束条件表示的可行域,以及所求表达式的几何意义是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
7.如图所示,已知$\overrightarrow{AC}=3\overrightarrow{BC}$,$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,$\overrightarrow{OC}$=$\overrightarrow c$,则下列等式中成立的是( )
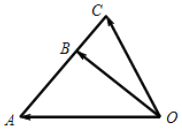

| A. | $\overrightarrow c=\frac{3}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow c=2\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow c=2\overrightarrow a-\overrightarrow b$ | D. | $\overrightarrow c=\frac{3}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
4.下列函数中为偶函数的是( )
| A. | y=x2sinx | B. | y=2-x | C. | y=$\frac{sinx}{x}$ | D. | y=|log0.5x| |
2.若点P(x,y)是区域$\left\{\begin{array}{l}1≤x+y≤3\\ 1≤y-x≤3\end{array}\right.$内的任意一点,且为直线y=kx上的点,则实数k的取值范围是( )
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |
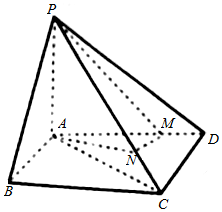 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4. 已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.
已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.