题目内容
9.如图所示是一个几何体的三视图,则这个几何体外接球的体积为( )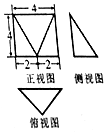
| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
分析 如图所示,该几何体为四棱锥P-ABCD,侧面PAB⊥底面ABCD,底面ABCD是正方形,其对角线AC∩BD=O,取AB的中点E,OE⊥AB,OE⊥侧面PAB,PE=2,AB=4.则点O为其外接球的球心,半径R=2$\sqrt{2}$.即可得出.
解答 解:如图所示,该几何体为四棱锥P-ABCD,侧面PAB⊥底面ABCD, 底面ABCD是正方形,其对角线AC∩BD=O,取AB的中点E,OE⊥AB,OE⊥侧面PAB,PE=2,AB=4.
底面ABCD是正方形,其对角线AC∩BD=O,取AB的中点E,OE⊥AB,OE⊥侧面PAB,PE=2,AB=4.
则点O为其外接球的球心,半径R=2$\sqrt{2}$.
∴这个几何体外接球的体积V=$\frac{4}{3}×π×(2\sqrt{2})^{3}$=$\frac{64\sqrt{2}}{3}$π.
故选:B.
点评 本题考查四棱锥的三视图、球的体积计算公式,了考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.设a=cos50°cos127°+cos40°cos37°,b=$\frac{\sqrt{2}}{2}$(sin56°-cos56°),c=$\frac{1-ta{n}^{2}39°}{1+ta{n}^{2}39°}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
4.设集合A={x|x2-3x<0},B={x|x2>4},则A∩B=( )
| A. | (-2,0) | B. | (-2,3) | C. | (0,2) | D. | (2,3) |
14.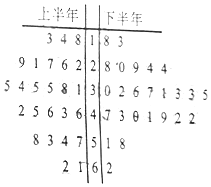 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
(Ⅰ)求该企业2016年一年生产一件产品的利润为10的概率;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元
自贡某工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示(如图).已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元(Ⅰ)求该企业2016年一年生产一件产品的利润为10的概率;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
1.若数列{an}满足an+1=2an(an≠0,n∈N*),且a3与a5的等差中项是10,则a1+a2+…+an等于( )
| A. | 2n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1-1 |
7.函数f(x)=3-sinx-2cos2x,$x∈[{\frac{π}{6},\frac{7π}{6}}]$,则函数的最大值与最小值之差为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{9}{8}$ |
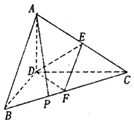 已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.
已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.