题目内容
如图,点 是椭圆
是椭圆 :
: 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 :
: 的直径,
的直径, 是过点
是过点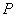 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 交圆
交圆 于
于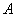 、
、 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 。
。
(I) 求椭圆 的方程;
的方程;
(II) 求△ 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 的方程。
的方程。

解:(1)由题意得 ∴椭圆
∴椭圆 的方程为
的方程为
(2)设
由题意知直线 的斜率存在,不妨设其为
的斜率存在,不妨设其为 ,则直线
,则直线 的方程为
的方程为 。故点
。故点 到直线
到直线 的距离为
的距离为 ,又圆
,又圆 :
: ,
,
∴ 又
又 , ∴直线
, ∴直线 的方程为
的方程为 由
由 ,消去
,消去 ,整理得
,整理得 ,
,
故 ,代入
,代入 的方程得
的方程得
 ∴
∴
设△ 的面积为
的面积为 , 则
, 则
∴
当且仅当 ,
,
即 时上式取等号。
时上式取等号。
∴当 时,△
时,△ 的面积取得最大值
的面积取得最大值 ,此时直线
,此时直线 的方程为
的方程为

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若方程
,若方程
 的取值范围是_____________________.
的取值范围是_____________________. ,集合
,集合 =
= ,
, =
= ,则
,则
 ( )
( ) B.
B. C.
C. D.
D.


 的首项
的首项 ,公差
,公差 ,数列
,数列 是等比数列,且
是等比数列,且 .
. 对任意正整数n,均有
对任意正整数n,均有 成立,求
成立,求 的值.
的值.