题目内容

1．函数f（x）=ln（x2+2）-ex-1的图象可能是（　　）
A．B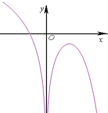．C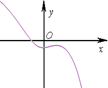．D．

分析 分析四个图象的不同，从而判断函数的性质，利用排除法求解．

解答 解：当x→+∞时，f（x）→-∞，
故排除D；
易知f（x）在R上连续，故排除B；
且f（0）=ln2-e-1＞0，
故排除C，
故选A．

点评 本题考查了函数的性质的判断与数形结合的思想方法应用．

练习册系列答案
相关题目
16．如果（1+x）n的展开式中x2的系数等于x的系数的3倍，则n的值为7．
12．已知f（x）是R奇函数，对x∈R都有f（x+4）=f（x）+f（2）成立，若f（1）=2，则f（2015）等于-2．
9．下列函数中，在其定义域上为增函数的是（　　）
A．y=x2B．y=e-xC．y=x-sinxD．y=-$\sqrt{x}$
16．下列有关命题的说法正确的是（　　）
A．命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
B．“x=-1”是“x2-5x-6=0”的必要不充分条件
C．命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R均有x2+x+1＜0”
D．已知命题p：?x∈[0，1]，a≥ex，命题q：?x∈R，使得x2+4x+a≤0．若命题“p∧q”是假命题，则实数a的取值范围是（-∞，e）∪（4，+∞）
6．已知$\overrightarrow a$=（cosθ，sinθ），$\overrightarrow b$=（-1，$\sqrt{3}$），则|$\overrightarrow a$-$2\overrightarrow b$|的最大值和最小值分别是（　　）
A．25，9B．5，3C．16，0D．16，4
13．已知函数f（x）=$\frac{x+a}{{x}^{2}+2x+2}$．
（I）证明：对任意实数a，存在（α，β），α＜β，使得函数f（x）在（α，β）上是增函数；
（Ⅱ）若方程f（x）=x-1有三个不同实数根，求实数a的取值范围．
10．若f（x）=3x3+2x2+x+4，则f（9）=2362．
1．如图，已知四边形ABEF为矩形，四边形ABCD为直角梯形，平面ABEF⊥平面ABCD，∠BAD=90°，AB∥CD，AF=BC=2，CD=3，AB=4．
（1）求证：AC⊥平面BCE；
（2）求三棱锥E-BCF的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网