题目内容
在△ABC中,A=
,C=
,b=2,那么a=( )
| π |
| 6 |
| 7π |
| 12 |
A、
| ||
| B、2 | ||
C、2
| ||
| D、1 |
考点:正弦定理
专题:解三角形
分析:利用三角形内角和求出B,通过正弦定理求解a.
解答:
解:∵在△ABC中,A=
,C=
,
∴B=π-
-
=
,
由正弦定理可得:a=
=
=
.
故选:A.
| π |
| 6 |
| 7π |
| 12 |
∴B=π-
| π |
| 6 |
| 7π |
| 12 |
| π |
| 4 |
由正弦定理可得:a=
| bsinA |
| sinB |
2×
| ||||
|
| 2 |
故选:A.
点评:本题考查正弦定理的应用,三角形的解法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知θ为锐角,且sin(θ-
)=
,在tanθ=( )
| π |
| 4 |
| ||
| 10 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
一质点沿直线运动,若由始点起经过t秒后的位移为s=
t3+
t2-4t+7,那么速度为0的时刻为( )
| 1 |
| 3 |
| 3 |
| 2 |
| A、0秒 | B、1秒末 |
| C、2秒末 | D、1秒末和2秒末 |
已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
x为实数,[x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则关于函数f(x)=x-[x],x∈R的说法不正确的是( )
| A、函数不具有奇偶性 | ||||
| B、x∈[1,2)时函数是增函数 | ||||
| C、函数是周期函数 | ||||
D、若函数g(x)=f(x)-kx恰有两个零点,则k∈(-∞,-1)∪(
|
x,y∈R,x∈[0,1],y∈[0,1],则x2≤y≤x的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x∈(-
,
),则函数y=tan(x+kπ),k∈Z与函数y=sinx的交点个数是( )
| π |
| 2 |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
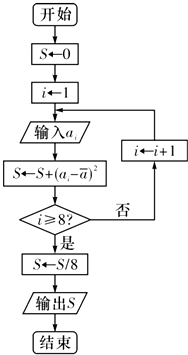 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.