题目内容
1．设幂函数f（x）=（m+3）xm，则f（2）-f（-2）=0．分析 利用幂函数的定义可得m，代入即可得出．
解答 解：由幂函数f（x）=（m+3）xm，则m+3=1，解得m=-2．
∴f（x）=x-2．
f（2）-f（-2）=$\frac{1}{{2}^{2}}-\frac{1}{（-2）^{2}}$=0．
故答案为：0．
点评 本题考查了幂函数的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
12．若$\overrightarrow a=（2cosα，1）$，$\overrightarrow b=（sinα，1）$，且$\overrightarrow a∥\overrightarrow b$，则tanα=（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -2 | D． | $-\frac{1}{2}$ |
9．已知函数f（x）=cos（cosx），下列结论错误的是（ ）
| A． | f（x）是奇函数 | B． | π为f（x）的最小正周期 | ||
| C． | f（x）的对称轴方程为x=kπ（k∈Z） | D． | f（x）的值域为[cos1，1] |
16．已知函数f（x）=ax2009+bsinx，且f（m）=2，则f（-m）=（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | -2 |
10．若sin（π+α）=$\frac{1}{2}$，α∈（-$\frac{π}{2}$，0），则tanα等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{3}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
11．
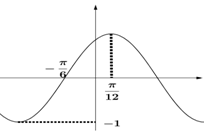已知f（x）=Asin（ωx+φ）（A＞0ω＞0，$|φ|＜\frac{π}{2}$，x∈R）在一个周期的图象如图所示，当$f（x）=\frac{1}{2}$时，$cos（2x-\frac{π}{6}）$=（ ）
已知f（x）=Asin（ωx+φ）（A＞0ω＞0，$|φ|＜\frac{π}{2}$，x∈R）在一个周期的图象如图所示，当$f（x）=\frac{1}{2}$时，$cos（2x-\frac{π}{6}）$=（ ）| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |