题目内容
已知圆心为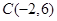 的圆经过点
的圆经过点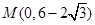 .
.
(1)求圆 的标准方程;
的标准方程;
(2)若直线 过点
过点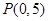 且被圆
且被圆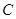 截得的线段长为
截得的线段长为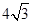 ,求直线
,求直线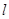 的方程;
的方程;
(3)是否存在斜率是1的直线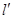 ,使得以
,使得以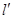 被圆
被圆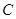 所截得的弦EF为直径的圆经过
所截得的弦EF为直径的圆经过
原点?若存在,试求出直线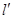 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
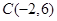 的圆经过点
的圆经过点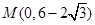 .
.(1)求圆
 的标准方程;
的标准方程;(2)若直线
 过点
过点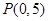 且被圆
且被圆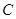 截得的线段长为
截得的线段长为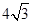 ,求直线
,求直线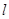 的方程;
的方程;(3)是否存在斜率是1的直线
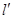 ,使得以
,使得以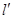 被圆
被圆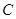 所截得的弦EF为直径的圆经过
所截得的弦EF为直径的圆经过原点?若存在,试求出直线
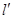 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(1) ;(2)
;(2)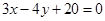 或
或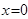 ;(3)不存在.
;(3)不存在.
 ;(2)
;(2)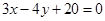 或
或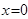 ;(3)不存在.
;(3)不存在.试题分析:(1)用两点的距离公式求出圆的半径,就可写出圆的标准方程;(2)法一:由圆的弦长可求得圆心到直线的距离,再用点斜式设出所求直线的方程,应用待定系数法:由点到直线的距离公式,就可求出所求直线的斜率,从而就可求得所求的直线方程,只是一定要注意:斜率不存在情形的讨论;法二:设出直线的斜率,写出直线方程,与圆方程联立,消去y得到关于x的一元二次方程,应用韦达定理及弦长公式,就可用斜率的代数式将弦长表示出来,从而获得关于斜率的方程解之即得;一样也需考虑斜率不存在情形;(3)法一:假设所求直线存在,先用斜截式设出其方程
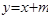 ,并用m的式子表示出弦EF的中点坐标,再画出图形,由以弦EF为直径的圆经过原点知
,并用m的式子表示出弦EF的中点坐标,再画出图形,由以弦EF为直径的圆经过原点知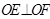 ,再作勾股定理即可获得关于m的方程,解此方程,有解则存在,并可写出对应直线方程,无解则不存在;法二:将直线方程与圆方程联立,消元,再用韦达定理,将条件
,再作勾股定理即可获得关于m的方程,解此方程,有解则存在,并可写出对应直线方程,无解则不存在;法二:将直线方程与圆方程联立,消元,再用韦达定理,将条件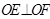 应用向量知识转化为
应用向量知识转化为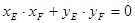 ,然后将韦达定理的结论代入即可获得关于m的方程,解此方程,有解则存在,并可写出对应直线方程,无解则不存在.
,然后将韦达定理的结论代入即可获得关于m的方程,解此方程,有解则存在,并可写出对应直线方程,无解则不存在.试题解析:(1)圆
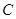 的半径为
的半径为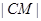
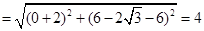 , 1分
, 1分 ∴圆
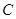 的标准方程为
的标准方程为 . 3分
. 3分(2)方法一 如图所示,设直线
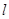 与圆
与圆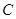 交于
交于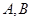 两点,且
两点,且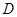 是
是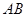 的中点,则
的中点,则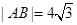 ,
,  且
且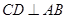 ,
,
∵圆
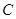 的半径为4,即
的半径为4,即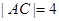
∴在
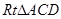 中,可得
中,可得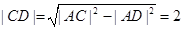 ,即点
,即点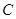 到直线
到直线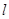 的距离为2. 4分
的距离为2. 4分(i)当所求直线
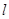 的斜率存在时,设所求直线的方程为
的斜率存在时,设所求直线的方程为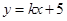 ,即
,即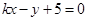 . 5分
. 5分由点到直线的距离公式得:
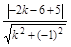 =2,解得
=2,解得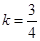 .
.∴此时直线
 的方程为
的方程为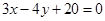 . 7分
. 7分(ii)当直线
 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为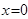 .
.将
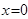 代入
代入 得
得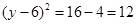 ,
,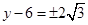 ,
,∴
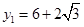 ,
,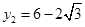 ,
,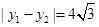
∴方程为
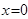 的直线也满足题意.
的直线也满足题意.∴所求直线
 的方程为
的方程为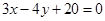 或
或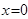 . 8分
. 8分方法二:当所求直线
 的斜率存在时,设所求直线的方程为
的斜率存在时,设所求直线的方程为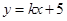 ,即
,即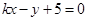 .---4分
.---4分联立直线与圆
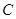 的方程:
的方程: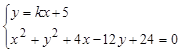 , 5分
, 5分消去
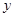 得
得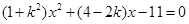 ①
①设方程①的两根为
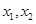 ,
,由根与系数的关系得
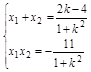 ②
②由弦长公式得
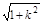 |x1-x2|=
|x1-x2|=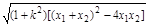 =4
=4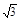 ③
③将②式代入③,并解得
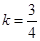 ,
,此时直线
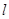 的方程为
的方程为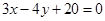 . 7分
. 7分当直线
 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为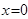 ,
,仿方法一验算得方程为
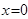 的直线也满足题意.
的直线也满足题意.∴所求直线
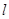 的方程为
的方程为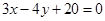 或
或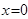 . 8分
. 8分(3)方法一:假设存在直线
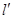 满足题设条件,设
满足题设条件,设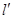 的方程为
的方程为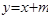 ,
,则
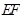 的中点
的中点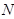 是两直线
是两直线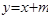 与
与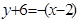 的交点,即
的交点,即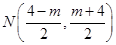 , 10分
, 10分∴
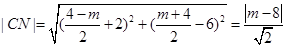 .
.∵以
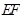 为直径的圆经过原点,
为直径的圆经过原点,∴
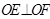 ,
,∴
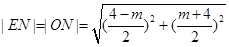 , 12分
, 12分又∵
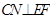 ,
,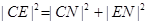 ,
,∴
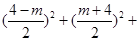
 ,化简得
,化简得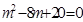 ,
,∵方程
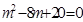 没有实数解,
没有实数解,∴不存在满足题设条件的直线
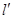 . 14分
. 14分方法二: 假设存在直线
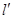 满足题设条件,并设
满足题设条件,并设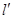 的方程为
的方程为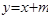 ,点
,点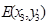 ,点
,点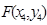 ,
,联立直线与圆
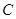 的方程
的方程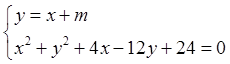 , 9分
, 9分消去
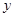 得
得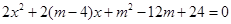
由根与系数的关系得
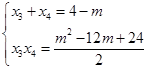 ④ 11分
④ 11分∵以
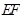 为直径的圆经过原点,
为直径的圆经过原点,∴
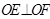 .
.若
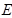 、
、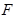 中有一点在
中有一点在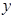 轴上,则另一点必在
轴上,则另一点必在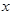 轴上,而在圆
轴上,而在圆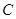 的方程中令
的方程中令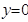 可得
可得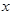 无实数解,故本情况不会出现. --------12分
无实数解,故本情况不会出现. --------12分∴
 即
即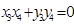 ,
,∴
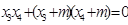 ,
,化简得:
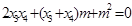 , 13分
, 13分以④代入并化简得
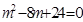
∵方程
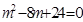 没有实数解,
没有实数解,∴不存在满足题设条件的直线
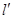 . 14分
. 14分
练习册系列答案
相关题目
 相切
相切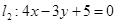 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长. :
: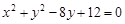 ,直线
,直线 经过点
经过点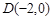 ,
, 为直径的圆
为直径的圆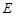 的方程;
的方程;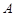 ,
,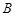 两点,且
两点,且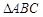 为等腰直角三角形,求直线
为等腰直角三角形,求直线 与曲线
与曲线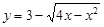 有公共点,则
有公共点,则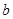 的取值范围是 .
的取值范围是 . 与圆
与圆 分别交于A,B两点.若
分别交于A,B两点.若 ,则实数
,则实数 的值为( ).
的值为( ).


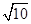 .
.